Given,

$$\alpha = \sum\limits_{k = 1}^\alpha {{{\sin }^{2k}}\left( {{\pi \over 6}} \right)} $$

$$ = {\sin ^2}\left( {{\pi \over 6}} \right) + {\sin ^4}\left( {{\pi \over 6}} \right) + {\sin ^6}\left( {{\pi \over 6}} \right)\, + \,......$$

This is a infinite G.P.

$$\therefore$$ $$\alpha = {{{{\sin }^2}\left( {{\pi \over 6}} \right)} \over {1 - {{\sin }^2}\left( {{\pi \over 6}} \right)}}$$

$$ = {{{1 \over 4}} \over {1 - {1 \over 4}}}$$

$$ = {1 \over 4} \times {4 \over 3}$$

$$ = {1 \over 3}$$

$$\therefore$$ $$g(x) = {2^{{x \over 3}}} + {2^{{1 \over 3}(1 - x)}}$$

Given $$x \in [0,1]$$

We know,

$$AM \ge GM$$

For $${2^{{x \over 3}}}$$ and $${2^{{1 \over 3}(1 - x)}}$$ both are positive in $$x \in [0,1]$$

$${{{x^{{x \over 3}}} + {2^{{1 \over 3}(1 - x)}}} \over 2} \ge {\left( {{2^{{x \over 3}}}\,.\,{2^{{1 \over 3}(1 - x)}}} \right)^{{1 \over 2}}}$$

$$ \Rightarrow {{{2^{{x \over 3}}} + {2^{{1 \over 3}(1 - x)}}} \over 2} \ge {\left( {{2^{{1 \over 3}}}} \right)^{{1 \over 2}}}$$

$$ \Rightarrow {2^{{x \over 3}}} + {2^{{1 \over 3}(1 - x)}} \ge 2\,.\,{2^{{1 \over 6}}}$$

$$ \Rightarrow g(x) \ge {2^{{7 \over 6}}}$$

We know, $$AM = GM$$ when terms are equal.

$$\therefore$$ $$g(x) = {2^{{7 \over 6}}}$$ when

$${2^{{x \over 3}}} = {2^{{1 \over 3}(1 - x)}}$$

$$ \Rightarrow {x \over 3} = {{1 - x} \over 3}$$

$$ \Rightarrow 2x = 1$$

$$ \Rightarrow x = {1 \over 2}$$

$$\therefore$$ At $$x = {1 \over 2}$$, $${\left[ {g(x)} \right]_{\min }} = {2^{{7 \over 6}}}$$

$$\therefore$$ Option (A) is correct.

And option (D) is wrong as at only at a single point $$x = {1 \over 2},\,g(x)$$ is minimum.

Now, $$g(x) = {2^{{x \over 3}}} + {2^{{1 \over 3}(1 - x)}}$$

$$ = {2^{{x \over 3}}} + {{{2^{{1 \over 3}}}} \over {{2^{{x \over 3}}}}}$$

$$ = {2^{{x \over 3}}} + {2^{{1 \over 3}}}\,.\,{2^{ - {x \over 3}}}$$

$$\therefore$$ $$g'(x) = {2^{{x \over 3}}}\,.\,\log 2\,.\,{1 \over 3} + {2^{{1 \over 3}}}\,.\,{2^{ - {x \over 3}}}\,.\,\log 2\,.\,\left( { - {1 \over 3}} \right)$$

$$ = {1 \over 3}\log 2\left[ {{2^{{x \over 3}}} - {{{2^{{1 \over 3}}}} \over {{2^{{x \over 3}}}}}} \right]$$

$$ = {1 \over 3}\log 2\left[ {{{{2^{{{2x} \over 3}}} + {2^{{1 \over 3}}}} \over {{2^{{x \over 3}}}}}} \right]$$

We already found that at $$x = {1 \over 2}$$ $$g(x)$$ is minimum.

$$\therefore$$ $$g'(x) = 0$$ at $$x = {1 \over 2}$$

Now, $$g'(x) > 0$$ when

$${1 \over 3}\log \left[ {{{{2^{{{2x} \over 3}}} - {2^{{1 \over 3}}}} \over {{2^{{x \over 3}}}}}} \right] > 0$$

$$ \Rightarrow {2^{{{2x} \over 3}}} > {2^{{1 \over 3}}}$$

$$ \Rightarrow {{2x} \over 3} > {1 \over 3}$$

$$ \Rightarrow x > {1 \over 2}$$

Similarly, $$g'(x) < 0$$ when $$x < {1 \over 2}$$

If we put it in number line we get this

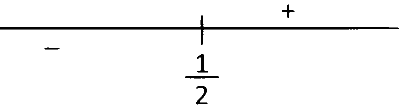
We know $$g'(x)$$ represent slope of curve $$g(x)$$ and it is negative when $$x < {1 \over 2}$$ and positive when $$x > {1 \over 2}$$ and zero when $$x = {1 \over 2}$$.

$$\therefore$$ Graph of $$g(x)$$ is

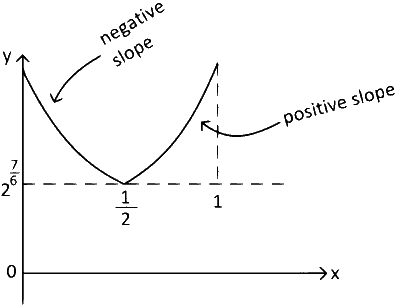
From graph you can see value of $$g(x)$$ is maximum either at $$x = 0$$ or $$x = 1$$ in the range $$x \in [0,1]$$.

$$\therefore$$ $$g(0) = {2^0} + {2^{{1 \over 3}}} = 1 + {2^{{1 \over 3}}}$$

$$g(1) = {2^{{1 \over 3}}} + {2^0} = 1 + {2^{{1 \over 3}}}$$

$$\therefore$$ We get maximum value at $$x = 0$$ and $$x = 1$$ both.

$$\therefore$$ B and C options are correct.