JEE Advance - Mathematics (2022 - Paper 1 Online - No. 3)
In a study about a pandemic, data of 900 persons was collected. It was found that
190 persons had symptom of fever,
220 persons had symptom of cough,
220 persons had symptom of breathing problem,
330 persons had symptom of fever or cough or both,
350 persons had symptom of cough or breathing problem or both,
340 persons had symptom of fever or breathing problem or both,
30 persons had all three symptoms (fever, cough and breathing problem).
If a person is chosen randomly from these 900 persons, then the probability that the person has at most one symptom is ____________.
190 persons had symptom of fever,
220 persons had symptom of cough,
220 persons had symptom of breathing problem,
330 persons had symptom of fever or cough or both,
350 persons had symptom of cough or breathing problem or both,
340 persons had symptom of fever or breathing problem or both,
30 persons had all three symptoms (fever, cough and breathing problem).
If a person is chosen randomly from these 900 persons, then the probability that the person has at most one symptom is ____________.
Answer
0.80
0.8
- OR
Explanation
Let person had symptom of fever $=n(F)=190$
Person had symptom of cough $=n(\mathrm{C})=220$
Person had symptom of breathing $=n(\mathrm{~B})=220$
Person had symptom of fever or cough
$$ =n(\mathrm{~F} \cup \mathrm{C})=330 $$
Person had symptom of cough or breathing
$$ =n(\mathrm{C} \cup \mathrm{B})=350 $$
Person had symptom of fever or breathing
$$ =n(\mathrm{~F} \cup \mathrm{B})=340 $$
Person had symptom of fever, cough and breathing $=n(\mathrm{~F} \cap \mathrm{C} \cup \mathrm{B})=30$
So $n(\mathrm{~F} \cap \mathrm{C})=n(\mathrm{~F})+n(\mathrm{C})-n(\mathrm{~F} \cup \mathrm{C})$
$=190+220-330$
$=80$
and
$ n(\mathrm{F} \cap \mathrm{B}) =n(\mathrm{~F})+n(\mathrm{~B})-n(\mathrm{~F} \cup \mathrm{B}) $
$ =190+220-340 $
$ =70 $
and $ n(\mathrm{C} \cap \mathrm{B}) =n(\mathrm{C})+n(\mathrm{~B})-n(\mathrm{C} \cap \mathrm{B}) $
$ =220+220-350 $
$ =90$
Number of people having at most one symptom
$$ =70+80+90+480 =720 $$
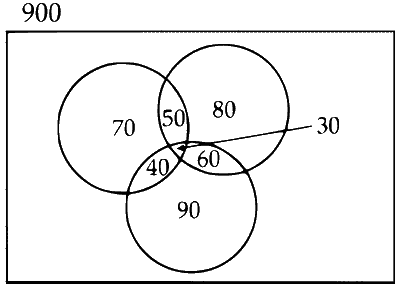
Required probability $=\frac{720}{900}=0.80$
Person had symptom of cough $=n(\mathrm{C})=220$
Person had symptom of breathing $=n(\mathrm{~B})=220$
Person had symptom of fever or cough
$$ =n(\mathrm{~F} \cup \mathrm{C})=330 $$
Person had symptom of cough or breathing
$$ =n(\mathrm{C} \cup \mathrm{B})=350 $$
Person had symptom of fever or breathing
$$ =n(\mathrm{~F} \cup \mathrm{B})=340 $$
Person had symptom of fever, cough and breathing $=n(\mathrm{~F} \cap \mathrm{C} \cup \mathrm{B})=30$
So $n(\mathrm{~F} \cap \mathrm{C})=n(\mathrm{~F})+n(\mathrm{C})-n(\mathrm{~F} \cup \mathrm{C})$
$=190+220-330$
$=80$
and
$ n(\mathrm{F} \cap \mathrm{B}) =n(\mathrm{~F})+n(\mathrm{~B})-n(\mathrm{~F} \cup \mathrm{B}) $
$ =190+220-340 $
$ =70 $
and $ n(\mathrm{C} \cap \mathrm{B}) =n(\mathrm{C})+n(\mathrm{~B})-n(\mathrm{C} \cap \mathrm{B}) $
$ =220+220-350 $
$ =90$
Number of people having at most one symptom
$$ =70+80+90+480 =720 $$

Required probability $=\frac{720}{900}=0.80$
Comments (0)


