JEE Advance - Mathematics (2022 - Paper 1 Online - No. 18)
Consider the ellipse
$$$ \frac{x^{2}}{4}+\frac{y^{2}}{3}=1 $$$
Let $H(\alpha, 0), 0<\alpha<2$, be a point. A straight line drawn through $H$ parallel to the $y$-axis crosses the ellipse and its auxiliary circle at points $E$ and $F$ respectively, in the first quadrant. The tangent to the ellipse at the point $E$ intersects the positive $x$-axis at a point $G$. Suppose the straight line joining $F$ and the origin makes an angle $\phi$ with the positive $x$-axis.
| List-I | List-II |
|---|---|
| (I) If $\phi=\frac{\pi}{4}$, then the area of the triangle $F G H$ is | (P) $\frac{(\sqrt{3}-1)^{4}}{8}$ |
| (II) If $\phi=\frac{\pi}{3}$, then the area of the triangle $F G H$ is | (Q) 1 |
| (III) If $\phi=\frac{\pi}{6}$, then the area of the triangle $F G H$ is | (R) $\frac{3}{4}$ |
| (IV) If $\phi=\frac{\pi}{12}$, then the area of the triangle $F G H$ is | (S) $\frac{1}{2 \sqrt{3}}$ |
| (T) $\frac{3 \sqrt{3}}{2}$ |
The correct option is:
$(\mathrm{I}) \rightarrow(\mathrm{R}) ;(\mathrm{II}) \rightarrow(\mathrm{S}) ;(\mathrm{III}) \rightarrow(\mathrm{Q}) ;(\mathrm{IV}) \rightarrow(\mathrm{P})$
(I) $\rightarrow$ (R); (II) $\rightarrow(\mathrm{T}) ;(\mathrm{III}) \rightarrow(\mathrm{S}) ;(\mathrm{IV}) \rightarrow(\mathrm{P})$
(I) $\rightarrow(\mathrm{Q}) ;(\mathrm{II}) \rightarrow(\mathrm{T}) ;(\mathrm{III}) \rightarrow(\mathrm{S}) ;(\mathrm{IV}) \rightarrow(\mathrm{P})$
(I) $\rightarrow$ (Q); (II) $\rightarrow$ (S); (III) $\rightarrow$ (Q); (IV) $\rightarrow$ (P)
Explanation
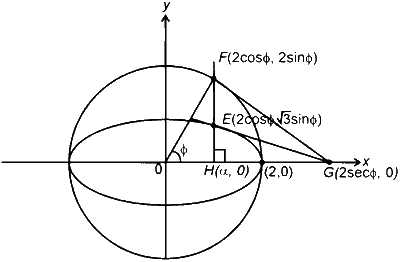
Given: $$ \frac{x^2}{4}+\frac{y^2}{3}=1 $$
Let $\quad \alpha=2 \cos \phi$
Tangent at $\mathrm{E}(2 \cos \phi, \sqrt{3} \sin \phi)$
to the ellipse is $\frac{x \cos \phi}{2}+\frac{y \sin \phi}{\sqrt{3}}=1$
This intersect $x$-axis at $\mathrm{G}(2 \sec \phi, 0)$
$$ \begin{aligned} & \text { Area of triangle } \mathrm{FGH}=\frac{1}{2}(2 \sec \phi-2 \cos \phi) 2 \sin \phi \\\\ & \Delta=2 \sin ^2 \phi \cdot \tan \phi \\\\ & \Delta=(1-\cos 2 \phi) \cdot \tan \phi \end{aligned} $$
$$ \begin{aligned} \text {I. If }\phi & =\frac{\pi}{4}, \Delta=1 \rightarrow Q \\\\ \text {II. If }\phi & =\frac{\pi}{3}, \Delta=2\left(\frac{\sqrt{3}}{2}\right)^2 \cdot \sqrt{3} \\\\ & =\frac{3 \sqrt{3}}{2} \rightarrow \mathrm{T} \end{aligned} $$
$$ \begin{aligned} \text {III. If }\phi & =\frac{\pi}{6}, \Delta=2\left(\frac{1}{2}\right)^2 \cdot \frac{1}{\sqrt{3}} \\\\ & =\frac{1}{2 \sqrt{3}} \rightarrow S \end{aligned} $$
$$ \begin{aligned} \text {IV. If }\phi=\frac{\pi}{12}, \Delta & =\left(1-\frac{\sqrt{3}}{2}\right) \cdot(2-\sqrt{3}) \\\\ & =\frac{(\sqrt{3}-1)^4}{8} \rightarrow P \end{aligned} $$
Comments (0)


