JEE Advance - Mathematics (2022 - Paper 1 Online - No. 13)
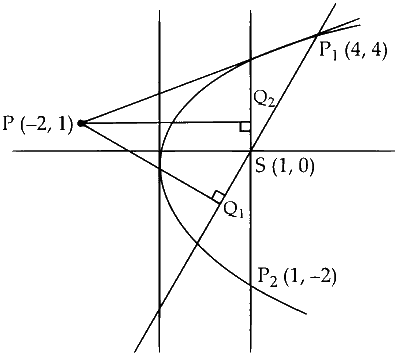
Consider the parabola $$y^{2}=4 x$$. Let $$S$$ be the focus of the parabola. A pair of tangents drawn to the parabola from the point $$P=(-2,1)$$ meet the parabola at $$P_{1}$$ and $$P_{2}$$. Let $$Q_{1}$$ and $$Q_{2}$$ be points on the lines $$S P_{1}$$ and $$S P_{2}$$ respectively such that $$P Q_{1}$$ is perpendicular to $$S P_{1}$$ and $$P Q_{2}$$ is perpendicular to $$S P_{2}$$. Then, which of the following is/are TRUE?
$$S Q_{1}=2$$
$$Q_{1} Q_{2}=\frac{3 \sqrt{10}}{5}$$
$$P Q_{1}=3$$
$$S Q_{2}=1$$
Explanation
Let $\mathrm{P}_1\left(t^2, 2 t\right)$ then tangent at $\mathrm{P}_1$ will be
$$ t y=x+t^2 $$
Since, it passes through $(-2,1)$
$$ \begin{aligned} & \Rightarrow t^2-t-2 =0 \\\\ & \Rightarrow t = 2,-1 \end{aligned} $$
So, we get point $\mathrm{P}_1(4, 4)$ and $\mathrm{P}_2(1, -2)$
Now finding the equation of $\mathrm{SP}_1: 4 x-3 y-4=0$
And equation of $\mathrm{SP}_2: x-1=0$
Now finding the point by foot of point on line formula,
$$ \mathrm{Q}_1: \frac{x_1+2}{4}=\frac{y_1-1}{-3}=\frac{-(-8-3-4)}{25}=\frac{3}{5} $$
We get $x_1=\frac{2}{5}, y_1=\frac{-4}{5}$ and $Q_2=(1,1)$
Now using the distance formula we get,
$$ \begin{aligned} & \mathrm{SQ}_1 =\sqrt{\left(1-\frac{2}{5}\right)^2+\left(\frac{4}{5}\right)^2}=1 \\\\ & \mathrm{Q}_1 \mathrm{Q}_2 =\sqrt{\frac{9}{25}+\frac{81}{25}}=\frac{3 \sqrt{10}}{5} \\\\ & \mathrm{PQ}_1 =\sqrt{\frac{144}{25}+\frac{81}{25}}=3 \\\\ & \mathrm{SQ}_2 =1 \end{aligned} $$
Hence, option (B, C, D) are correct.
$$ t y=x+t^2 $$

Since, it passes through $(-2,1)$
$$ \begin{aligned} & \Rightarrow t^2-t-2 =0 \\\\ & \Rightarrow t = 2,-1 \end{aligned} $$
So, we get point $\mathrm{P}_1(4, 4)$ and $\mathrm{P}_2(1, -2)$
Now finding the equation of $\mathrm{SP}_1: 4 x-3 y-4=0$
And equation of $\mathrm{SP}_2: x-1=0$
Now finding the point by foot of point on line formula,
$$ \mathrm{Q}_1: \frac{x_1+2}{4}=\frac{y_1-1}{-3}=\frac{-(-8-3-4)}{25}=\frac{3}{5} $$
We get $x_1=\frac{2}{5}, y_1=\frac{-4}{5}$ and $Q_2=(1,1)$
Now using the distance formula we get,
$$ \begin{aligned} & \mathrm{SQ}_1 =\sqrt{\left(1-\frac{2}{5}\right)^2+\left(\frac{4}{5}\right)^2}=1 \\\\ & \mathrm{Q}_1 \mathrm{Q}_2 =\sqrt{\frac{9}{25}+\frac{81}{25}}=\frac{3 \sqrt{10}}{5} \\\\ & \mathrm{PQ}_1 =\sqrt{\frac{144}{25}+\frac{81}{25}}=3 \\\\ & \mathrm{SQ}_2 =1 \end{aligned} $$
Hence, option (B, C, D) are correct.
Comments (0)


