Given, $${3 \over 2}{\cos ^{ - 1}}\sqrt {{2 \over {2 + {\pi ^2}}}} + {1 \over 4}{\sin ^{ - 1}}\left( {{{2\sqrt 2 \pi } \over {2 + {\pi ^2}}}} \right) + {\tan ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)$$

Let, $${\tan ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right) = \alpha $$

$$ \Rightarrow {{\sqrt 2 } \over \pi } = \tan \alpha $$

We know, $$\sin 2\alpha = {{2\tan \alpha } \over {1 + {{\tan }^2}\alpha }}$$

$$ = {{2\left( {{{\sqrt 2 } \over \pi }} \right)} \over {1 + {2 \over {{\pi ^2}}}}}$$

$$ = {{2\sqrt 2 \pi } \over {2 + {\pi ^2}}}$$

$$ \Rightarrow 2\alpha = {\sin ^{ - 1}}\left( {{{2\sqrt 2 \pi } \over {2 + {\pi ^2}}}} \right) = 2{\tan ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)$$

Now, let, $${\cos ^{ - 1}}\left( {\sqrt {{2 \over {2 + {\pi ^2}}}} } \right) = \beta $$

$$ \Rightarrow \sqrt {{2 \over {2 + {\pi ^2}}}} = \cos \beta $$

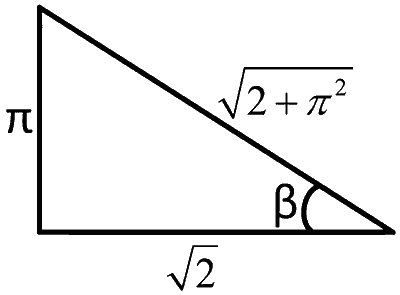
$$\therefore$$ $$\cot \beta = {{\sqrt 2 } \over \pi }$$

$$ \Rightarrow \beta = {\cot ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)$$

$$\therefore$$ $${\cos ^{ - 1}}\left( {\sqrt {{2 \over {2 + {\pi ^2}}}} } \right) = {\cot ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)$$

$$\therefore$$ $${3 \over 2}{\cos ^{ - 1}}\left( {\sqrt {{2 \over {2 + {\pi ^2}}}} } \right) + {1 \over 4}{\sin ^{ - 1}}\left( {{{2\sqrt 2 \pi } \over {2 + {\pi ^2}}}} \right) + {\tan ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)$$

$$ = {3 \over 2}{\cot ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right) + {1 \over 4}\left( {2 + \tan \left( {{{\sqrt 2 } \over \pi }} \right)} \right) + {\tan ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)$$

$$ = {3 \over 2}{\cot ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right) + {1 \over 2}{\tan ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right) + {\tan ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)$$

$$ = {3 \over 2}{\cot ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right) + {3 \over 2}{\tan ^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)$$

$$ = {3 \over 2}\left( {{{\tan }^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right) + {{\cot }^{ - 1}}\left( {{{\sqrt 2 } \over \pi }} \right)} \right)$$

$$ = {3 \over 2} \times {\pi \over 2}$$

$$ = {{3\pi } \over 4}$$

$$ = 2.36$$