JEE Advance - Mathematics (2021 - Paper 2 Online - No. 7)
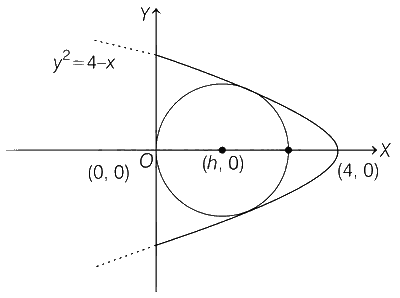
Consider the region R = {(x, y) $$\in$$ R $$\times$$ R : x $$\ge$$ 0 and y2 $$\le$$ 4 $$-$$ x}. Let F be the family of all circles that are contained in R and have centers on the x-axis. Let C be the circle that has largest radius among the circles in F. Let ($$\alpha$$, $$\beta$$) be a point where the circle C meets the curve y2 = 4 $$-$$ x.
The radius of the circle C is ___________.
The radius of the circle C is ___________.
Answer
1.50
Explanation
Given, x $$\ge$$ 0, y2 $$\le$$ 4 $$-$$ x
Let equation of circle be
(x $$-$$ h)2 + y2 = h2 .... (i)
Solving Eq. (i) with y2 = 4 $$-$$ x, we get
x2 $$-$$ 2hx + 4 $$-$$ x = 0
$$\Rightarrow$$ x2 $$-$$ x(2h + 1) + 4 = 0 .... (ii)
For touching/tangency, Discriminant (D) = 0
i.e. (2h + 1)2 = 16 $$\Rightarrow$$ 2h + 1 = $$\pm$$ 4
$$\Rightarrow$$ 2h = $$\pm$$ 4 $$-$$ 1
$$\Rightarrow$$ $$h = {3 \over 2},h = {{ - 5} \over 2}$$ (Rejected) because part of circle lies outside R. So, $$h = {3 \over 2}$$ = radius of circle (C).
Let equation of circle be
(x $$-$$ h)2 + y2 = h2 .... (i)

Solving Eq. (i) with y2 = 4 $$-$$ x, we get
x2 $$-$$ 2hx + 4 $$-$$ x = 0
$$\Rightarrow$$ x2 $$-$$ x(2h + 1) + 4 = 0 .... (ii)
For touching/tangency, Discriminant (D) = 0
i.e. (2h + 1)2 = 16 $$\Rightarrow$$ 2h + 1 = $$\pm$$ 4
$$\Rightarrow$$ 2h = $$\pm$$ 4 $$-$$ 1
$$\Rightarrow$$ $$h = {3 \over 2},h = {{ - 5} \over 2}$$ (Rejected) because part of circle lies outside R. So, $$h = {3 \over 2}$$ = radius of circle (C).
Comments (0)


