JEE Advance - Mathematics (2021 - Paper 2 Online - No. 6)
Let E denote the parabola y2 = 8x. Let P = ($$-$$2, 4), and let Q and Q' be two distinct points on E such that the lines PQ and PQ' are tangents to E. Let F be the focus of E. Then which of the following statements is(are) TRUE?
The triangle PFQ is a right-angled triangle
The triangle QPQ' is a right-angled triangle
The distance between P and F is 5$$\sqrt 2 $$
F lies on the line joining Q and Q'
Explanation
Given, E : y2 = 8x .... (i)
and P $$\equiv$$ ($$-$$2, 4)
Now, directrix of Eq. (i) is x = $$-$$2
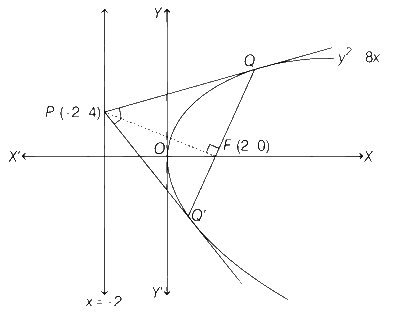
So, point P($$-$$2, 4) lies on the directrix of parabola y2 = 8x. Hence, $$\angle QPQ' = {\pi \over 2}$$ (by the definition of director circle) and chord QQ' is a focal chord and segment PQ subtends a right angle at the focus.
Slope of PF = $$-$$1 ($$\because$$ PF $$\bot$$ QQ')
Now, slope of $$QQ' = {2 \over {{t_1} + {t_2}}} = 1$$
$$\therefore$$ $$PF = \sqrt {{{(2 + 2)}^2} + {{(0 + 4)}^2}} = \sqrt {32} = 4\sqrt 2 $$
and P $$\equiv$$ ($$-$$2, 4)
Now, directrix of Eq. (i) is x = $$-$$2

So, point P($$-$$2, 4) lies on the directrix of parabola y2 = 8x. Hence, $$\angle QPQ' = {\pi \over 2}$$ (by the definition of director circle) and chord QQ' is a focal chord and segment PQ subtends a right angle at the focus.
Slope of PF = $$-$$1 ($$\because$$ PF $$\bot$$ QQ')
Now, slope of $$QQ' = {2 \over {{t_1} + {t_2}}} = 1$$
$$\therefore$$ $$PF = \sqrt {{{(2 + 2)}^2} + {{(0 + 4)}^2}} = \sqrt {32} = 4\sqrt 2 $$
Comments (0)


