JEE Advance - Mathematics (2021 - Paper 2 Online - No. 2)
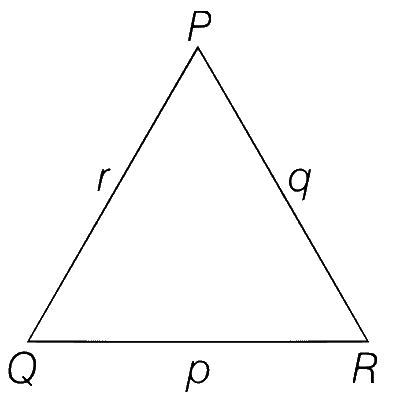
Consider a triangle PQR having sides of lengths p, q and r opposite to the angles P, Q and R, respectively. Then which of the following statements is (are) TRUE?
$$\cos P \ge 1 - {{{p^2}} \over {2qr}}$$
$$\cos R \ge \left( {{{q - r} \over {p + q}}} \right)\cos P + \left( {{{p - r} \over {p + q}}} \right)\cos Q$$
$${{q + r} \over p} < 2{{\sqrt {\sin q\sin R} } \over {\sin P}}$$
If p < q and p < r, then $$\cos Q > {p \over r}$$ and $$\cos R > {p \over q}$$
Explanation
For option (a) $$\cos P = {{{q^2} + {r^2} - {p^2}} \over {2qr}}$$ ..... (i)
$$\because$$ $${{{q^2} + {r^2}} \over 2} \ge \sqrt {{q^2}{r^2}} (AM \ge GM)$$
$$ \Rightarrow {q^2} + {r^2} \ge 2qr$$
From Eq. (i), we get
$$\cos P \ge {{2qr - {p^2}} \over {2qr}}$$
$$ \Rightarrow \cos P \ge 1 - {{{p^2}} \over {2qr}}$$ $$\to$$ option (a) is correct.
For option (b)
$${{(q - r)\cos P + (p - r)\cos Q} \over {p + q}}$$$$ = {{(q\cos P + p\cos Q) - r(\cos P + \cos Q)} \over {p + q}}$$
$$ \Rightarrow 4{\lambda ^2} - 2\lambda = 0$$
$$ \Rightarrow u\,.\,v\, = 0$$ (Rejected)
or $$u\,.\,v = {1 \over 2}$$
$$\therefore$$ $$u\,.\,v = {1 \over 2}$$
$$\therefore$$ $${\left| {3u + 5v} \right|^2} = 9{\left| u \right|^2} + 25{\left| v \right|^2} + 3 \times 5 \times 2 \times u\,.\,v$$
$$ = 9 + 25 + 30 \times {1 \over 2}$$
$$ = 49$$ ($$\because$$ $$\left| u \right| = \left| v \right| = 1$$, given)
$$\therefore$$ $$\left| {3u + 5v} \right| = 7$$
$$ = {{r - r(\cos P + \cos Q)} \over {p + q}} = {{r - r\cos P - r\cos Q} \over {p + q}}$$
$$ = {{r - (q - \cos R) - (p - q\cos R)} \over {p + q}}$$
$$ = {{(r - p - q) + (p + q)\cos R} \over {p + q}}$$
$$ = \cos R + {{r - (p + q)} \over {p + q}} \le \cos R$$ ($$\because$$ $$r < p + q$$)
Hence, option (b) is correct.
For option (c)
$${{q + r} \over p} = {{\sin Q + \sin R} \over {\sin P}} \ge {{2\sqrt {\sin Q.\sin R} } \over {\sin P}}$$
$$\to$$ option (c) is incorrect.
For option (d)
If p < q and p < r, then p is the smallest side and hence one of Q or R can be obtuse.
So, one of cos Q and cos R can be negative.
Therefore, $$\cos Q > {p \over r}$$ and $$\cos R > {p \over q}$$ cannot hold always.
Option (d) is incorrect.

$$\because$$ $${{{q^2} + {r^2}} \over 2} \ge \sqrt {{q^2}{r^2}} (AM \ge GM)$$
$$ \Rightarrow {q^2} + {r^2} \ge 2qr$$
From Eq. (i), we get
$$\cos P \ge {{2qr - {p^2}} \over {2qr}}$$
$$ \Rightarrow \cos P \ge 1 - {{{p^2}} \over {2qr}}$$ $$\to$$ option (a) is correct.
For option (b)
$${{(q - r)\cos P + (p - r)\cos Q} \over {p + q}}$$$$ = {{(q\cos P + p\cos Q) - r(\cos P + \cos Q)} \over {p + q}}$$
$$ \Rightarrow 4{\lambda ^2} - 2\lambda = 0$$
$$ \Rightarrow u\,.\,v\, = 0$$ (Rejected)
or $$u\,.\,v = {1 \over 2}$$
$$\therefore$$ $$u\,.\,v = {1 \over 2}$$
$$\therefore$$ $${\left| {3u + 5v} \right|^2} = 9{\left| u \right|^2} + 25{\left| v \right|^2} + 3 \times 5 \times 2 \times u\,.\,v$$
$$ = 9 + 25 + 30 \times {1 \over 2}$$
$$ = 49$$ ($$\because$$ $$\left| u \right| = \left| v \right| = 1$$, given)
$$\therefore$$ $$\left| {3u + 5v} \right| = 7$$
$$ = {{r - r(\cos P + \cos Q)} \over {p + q}} = {{r - r\cos P - r\cos Q} \over {p + q}}$$
$$ = {{r - (q - \cos R) - (p - q\cos R)} \over {p + q}}$$
$$ = {{(r - p - q) + (p + q)\cos R} \over {p + q}}$$
$$ = \cos R + {{r - (p + q)} \over {p + q}} \le \cos R$$ ($$\because$$ $$r < p + q$$)
Hence, option (b) is correct.
For option (c)
$${{q + r} \over p} = {{\sin Q + \sin R} \over {\sin P}} \ge {{2\sqrt {\sin Q.\sin R} } \over {\sin P}}$$
$$\to$$ option (c) is incorrect.
For option (d)
If p < q and p < r, then p is the smallest side and hence one of Q or R can be obtuse.
So, one of cos Q and cos R can be negative.
Therefore, $$\cos Q > {p \over r}$$ and $$\cos R > {p \over q}$$ cannot hold always.
Option (d) is incorrect.
Comments (0)


