JEE Advance - Mathematics (2021 - Paper 2 Online - No. 12)
Let $${g_i}:\left[ {{\pi \over 8},{{3\pi } \over 8}} \right] \to R,i = 1,2$$, and $$f:\left[ {{\pi \over 8},{{3\pi } \over 8}} \right] \to R$$ be functions such that $${g_1}(x) = 1,{g_2}(x) = |4x - \pi |$$ and $$f(x) = {\sin ^2}x$$, for all $$x \in \left[ {{\pi \over 8},{{3\pi } \over 8}} \right]$$. Define $${S_i} = \int\limits_{{\pi \over 8}}^{{{3\pi } \over 8}} {f(x).{g_i}(x)dx} $$, i = 1, 2
The value of $${{48{S_2}} \over {{\pi ^2}}}$$ is ___________.
The value of $${{48{S_2}} \over {{\pi ^2}}}$$ is ___________.
Answer
1.50
Explanation
$${S_2} = \int\limits_{\pi /8}^{3\pi /8} {{{\sin }^2}x\left| {4x - \pi } \right|dx} $$ .... (i)
$${S_2} = \int_{\pi /8}^{3\pi /8} {{{\sin }^2}\left( {{{3\pi } \over 8} + {\pi \over 8} - x} \right)\left| {4\left( {{{3\pi } \over 8} + {\pi \over 8} - x} \right) - \pi } \right|dx} $$
$$[\int_a^b {f(x)dx = \int_a^b {f(a + b - x)dx]} } $$
$$ \Rightarrow {S_2} = \int_{\pi /8}^{3\pi /8} {{{\cos }^2}x\left| {\pi - 4x} \right|dx} $$ .... (ii)
Adding Eqs. (i) and (ii), we get
$$2{S_2} = \int_{\pi /8}^{3\pi /8} {\left| {4x - \pi } \right|dx} $$
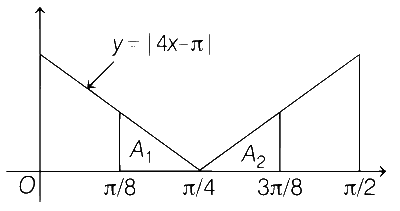
From figure,
$${A_1} = {1 \over 2} \times {\pi \over 8} \times {\pi \over 2} = {{{\pi ^2}} \over {32}} = {A_2}$$
$$\therefore$$ $$2{S_2} = 2{A_1} = {{{\pi ^2}} \over {16}} \Rightarrow {S_2} = {{{\pi ^2}} \over {32}}$$
Hence, $${{48{S_2}} \over {{\pi ^2}}} = {{48} \over {32}} = {3 \over 2} = 1.5$$
$${S_2} = \int_{\pi /8}^{3\pi /8} {{{\sin }^2}\left( {{{3\pi } \over 8} + {\pi \over 8} - x} \right)\left| {4\left( {{{3\pi } \over 8} + {\pi \over 8} - x} \right) - \pi } \right|dx} $$

$$[\int_a^b {f(x)dx = \int_a^b {f(a + b - x)dx]} } $$
$$ \Rightarrow {S_2} = \int_{\pi /8}^{3\pi /8} {{{\cos }^2}x\left| {\pi - 4x} \right|dx} $$ .... (ii)
Adding Eqs. (i) and (ii), we get
$$2{S_2} = \int_{\pi /8}^{3\pi /8} {\left| {4x - \pi } \right|dx} $$
From figure,
$${A_1} = {1 \over 2} \times {\pi \over 8} \times {\pi \over 2} = {{{\pi ^2}} \over {32}} = {A_2}$$
$$\therefore$$ $$2{S_2} = 2{A_1} = {{{\pi ^2}} \over {16}} \Rightarrow {S_2} = {{{\pi ^2}} \over {32}}$$
Hence, $${{48{S_2}} \over {{\pi ^2}}} = {{48} \over {32}} = {3 \over 2} = 1.5$$
Comments (0)


