JEE Advance - Mathematics (2021 - Paper 1 Online - No. 4)
Let $\theta_1, \theta_2, \ldots, \theta_{10}$ be positive valued angles (in radian) such that $\theta_1+\theta_2+\cdots+\theta_{10}=2 \pi$. Define the complex numbers $z_1=e^{i \theta_1}, z_k=z_{k-1} e^{i \theta_k}$ for $k=2,3, \ldots, 10$, where $i=\sqrt{-1}$. Consider the statements $P$ and $Q$ given below:
$$P:\left| {{z_2} - {z_1}} \right| + \left| {{z_3} - {z_2}} \right| + ..... + \left| {{z_{10}} - {z_9}} \right| + \left| {{z_1} - {z_{10}}} \right| \le 2\pi $$
$$Q:\left| {z_2^2 - z_1^2} \right| + \left| {z_3^2 - z_2^2} \right| + .... + \left| {z_{10}^2 - z_9^2} \right| + \left| {z_1^2 - z_{10}^2} \right| \le 4\pi $$
Then,
$$P:\left| {{z_2} - {z_1}} \right| + \left| {{z_3} - {z_2}} \right| + ..... + \left| {{z_{10}} - {z_9}} \right| + \left| {{z_1} - {z_{10}}} \right| \le 2\pi $$
$$Q:\left| {z_2^2 - z_1^2} \right| + \left| {z_3^2 - z_2^2} \right| + .... + \left| {z_{10}^2 - z_9^2} \right| + \left| {z_1^2 - z_{10}^2} \right| \le 4\pi $$
Then,
P is TRUE and Q is FALSE
Q is TRUE and P is FALSE
both P and Q are TRUE
both P and Q are FALSE
Explanation
Both P and Q are true.
$$\because$$ Length of direct ditance $$\le$$ length of arc
i.e. | z2 $$-$$ z1 | = length of line AB $$\le$$ length of arc AB.
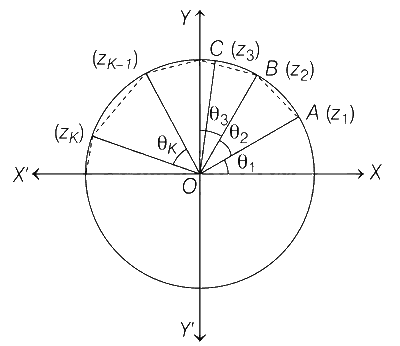
| z3 $$-$$ z2 | = length of line BC $$\le$$ length of arc BC.
$$\therefore$$ Sum of length of these 10 lines $$\le$$ sum of length of arcs (i.e. 2$$\pi$$) (because $$\theta$$1 + $$\theta$$2 + $$\theta$$3 + .... + $$\theta$$10 = 2$$\pi$$ (given)
$$\therefore$$ | z2 $$-$$ z1 | + | z3 $$-$$ z2 | + ..... + | z1 $$-$$ z10 | $$\le$$ 2$$\pi$$ $$\to$$ P is true.
And | z$$_k^2$$ $$-$$ z$$_{k - 1}^2$$ | = | zk $$-$$ zk $$-$$ 1 | | zk + zk $$-$$ 1 |
As we know that,
| zk + zk $$-$$ 1 | $$\le$$ | zk | + | zk $$-$$ 1 | $$\le$$ 2
$$\therefore$$ | z$$_2^2$$ $$-$$ z$$_1^2$$ | + | z$$_3^2$$ $$-$$ z$$_2^2$$ | + .... + | z$$_1^2$$ $$-$$ z$$_{10}^2$$ | $$\le$$ 2 ( | z2 $$-$$ z1 | + | z3 $$-$$ z2 | + .... + | z1 $$-$$ z10 | )
$$\le$$ 2(2$$\pi$$)
$$\le$$ 4$$\pi$$ $$\to$$ Q is true.
$$\because$$ Length of direct ditance $$\le$$ length of arc
i.e. | z2 $$-$$ z1 | = length of line AB $$\le$$ length of arc AB.

| z3 $$-$$ z2 | = length of line BC $$\le$$ length of arc BC.
$$\therefore$$ Sum of length of these 10 lines $$\le$$ sum of length of arcs (i.e. 2$$\pi$$) (because $$\theta$$1 + $$\theta$$2 + $$\theta$$3 + .... + $$\theta$$10 = 2$$\pi$$ (given)
$$\therefore$$ | z2 $$-$$ z1 | + | z3 $$-$$ z2 | + ..... + | z1 $$-$$ z10 | $$\le$$ 2$$\pi$$ $$\to$$ P is true.
And | z$$_k^2$$ $$-$$ z$$_{k - 1}^2$$ | = | zk $$-$$ zk $$-$$ 1 | | zk + zk $$-$$ 1 |
As we know that,
| zk + zk $$-$$ 1 | $$\le$$ | zk | + | zk $$-$$ 1 | $$\le$$ 2
$$\therefore$$ | z$$_2^2$$ $$-$$ z$$_1^2$$ | + | z$$_3^2$$ $$-$$ z$$_2^2$$ | + .... + | z$$_1^2$$ $$-$$ z$$_{10}^2$$ | $$\le$$ 2 ( | z2 $$-$$ z1 | + | z3 $$-$$ z2 | + .... + | z1 $$-$$ z10 | )
$$\le$$ 2(2$$\pi$$)
$$\le$$ 4$$\pi$$ $$\to$$ Q is true.
Comments (0)


