JEE Advance - Mathematics (2021 - Paper 1 Online - No. 2)
The area of the region
$$\left\{ {\matrix{ {(x,y):0 \le x \le {9 \over 4},} & {0 \le y \le 1,} & {x \ge 3y,} & {x + y \ge 2} \cr } } \right\}$$ is
$$\left\{ {\matrix{ {(x,y):0 \le x \le {9 \over 4},} & {0 \le y \le 1,} & {x \ge 3y,} & {x + y \ge 2} \cr } } \right\}$$ is
$${{11} \over {32}}$$
$${{35} \over {96}}$$
$${{37} \over {96}}$$
$${{13} \over {32}}$$
Explanation
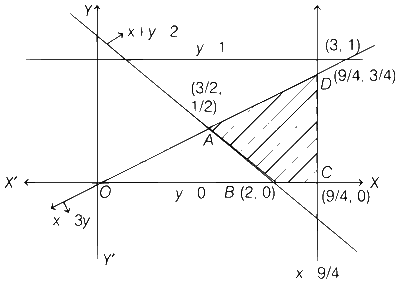
Required area = Shaded region
On solving x + y = 2 and x = 3y, we get
$$A \equiv \left( {{3 \over 2},{1 \over 2}} \right)$$
On solving y = 0 and x + y = 2, we get
B ≡ (2, 0)
On solving x = $${9 \over 4}$$ and x = 3y, we get
D ≡ $$\left( {{9 \over 4},{3 \over 4}} \right)$$
and C ≡ $$\left( {{9 \over 4},0} \right)$$
Required area = Area of ∆OCD − Area of ∆OBA
= $${1 \over 2} \times \left( {{9 \over 4} - 0} \right) \times {3 \over 4} - {1 \over 2} \times \left( {2 - 0} \right) \times {1 \over 2}$$
= $${{27} \over {32}} - {1 \over 2}$$
= $${{11} \over {32}}$$
Comments (0)


