JEE Advance - Mathematics (2021 - Paper 1 Online - No. 18)
In a triangle ABC, let AB = $$\sqrt {23} $$, BC = 3 and CA = 4. Then the value of $${{\cot A + \cot C} \over {\cot B}}$$ is _________.
Answer
2
Explanation
Given,
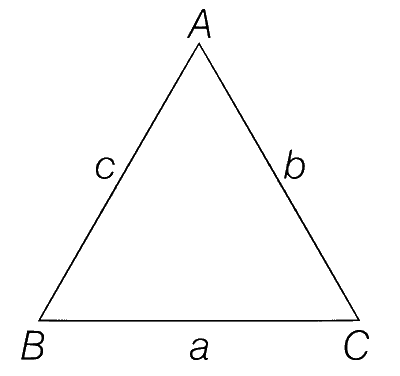
$$AB = \sqrt {23} = c$$
$$BC = 3 = a$$
$$CA = 4 = b$$
Now,
$${{\cot A + \cot C} \over {\cot B}} = {{{{\cos A} \over {\sin A}} + {{\cos C} \over {\sin C}}} \over {{{\cos B} \over {\sin B}}}}$$
$$ = {{{{{b^2} + {c^2} - {a^2}} \over {2bc(\sin A)}} + {{{a^2} + {b^2} - {c^2}} \over {2ab(\sin C)}}} \over {{{{c^2} + {a^2} - {b^2}} \over {2ac(\sin B)}}}}$$
$$ = {{{{{b^2} + {c^2} - {a^2}} \over {4\Delta }} + {{{a^2} + {b^2} - {c^2}} \over {4\Delta }}} \over {{{{c^2} + {a^2} - {b^2}} \over {4\Delta }}}}$$
$$ = {{{b^2} + {c^2} - {a^2} + {a^2} + {b^2} - {c^2}} \over {{c^2} + {a^2} - {b^2}}}$$
$$ = {{2{b^2}} \over {{a^2} + {c^2} - {b^2}}} = {{2 \times 16} \over {9 + 23 - 16}} = {{32} \over {16}} = 2$$
$$AB = \sqrt {23} = c$$
$$BC = 3 = a$$
$$CA = 4 = b$$

Now,
$${{\cot A + \cot C} \over {\cot B}} = {{{{\cos A} \over {\sin A}} + {{\cos C} \over {\sin C}}} \over {{{\cos B} \over {\sin B}}}}$$
$$ = {{{{{b^2} + {c^2} - {a^2}} \over {2bc(\sin A)}} + {{{a^2} + {b^2} - {c^2}} \over {2ab(\sin C)}}} \over {{{{c^2} + {a^2} - {b^2}} \over {2ac(\sin B)}}}}$$
$$ = {{{{{b^2} + {c^2} - {a^2}} \over {4\Delta }} + {{{a^2} + {b^2} - {c^2}} \over {4\Delta }}} \over {{{{c^2} + {a^2} - {b^2}} \over {4\Delta }}}}$$
$$ = {{{b^2} + {c^2} - {a^2} + {a^2} + {b^2} - {c^2}} \over {{c^2} + {a^2} - {b^2}}}$$
$$ = {{2{b^2}} \over {{a^2} + {c^2} - {b^2}}} = {{2 \times 16} \over {9 + 23 - 16}} = {{32} \over {16}} = 2$$
Comments (0)


