JEE Advance - Mathematics (2021 - Paper 1 Online - No. 16)
For any complex number w = c + id, let $$\arg (w) \in ( - \pi ,\pi ]$$, where $$i = \sqrt { - 1} $$. Let $$\alpha$$ and $$\beta$$ be real numbers such that for all complex numbers z = x + iy satisfying $$\arg \left( {{{z + \alpha } \over {z + \beta }}} \right) = {\pi \over 4}$$, the ordered pair (x, y) lies on the circle $${x^2} + {y^2} + 5x - 3y + 4 = 0$$, Then which of the following statements is (are) TRUE?
$$\alpha$$ = $$-$$1
$$\alpha$$$$\beta$$ = 4
$$\alpha$$$$\beta$$ = $$-$$4
$$\beta$$ = 4
Explanation
Circle $${x^2} + {y^2} + 5x - 3y + 4 = 0$$ cuts the real axis (X-axis) at ($$-$$4, 0), ($$-$$1, 0).
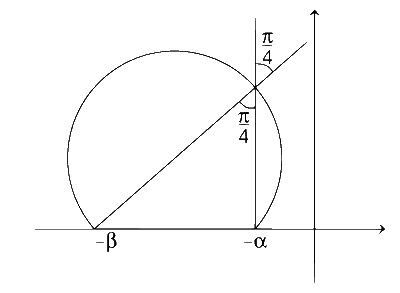
$$\arg \left( {{{z + \alpha } \over {z + \beta }}} \right) = {\pi \over 4}$$ implies z is on arc and ($$-$$ $$\alpha$$, 0) and ($$-$$ $$\beta$$, 0) subtend $${\pi \over 4}$$ on z.
So, $$\alpha$$ = 1 and $$\beta$$ = 4
Hence, $$\alpha$$$$\beta$$ = 1 $$\times$$ 4 = 4 and $$\beta$$ = 4

$$\arg \left( {{{z + \alpha } \over {z + \beta }}} \right) = {\pi \over 4}$$ implies z is on arc and ($$-$$ $$\alpha$$, 0) and ($$-$$ $$\beta$$, 0) subtend $${\pi \over 4}$$ on z.
So, $$\alpha$$ = 1 and $$\beta$$ = 4
Hence, $$\alpha$$$$\beta$$ = 1 $$\times$$ 4 = 4 and $$\beta$$ = 4
Comments (0)


