JEE Advance - Mathematics (2021 - Paper 1 Online - No. 12)
Let f : R $$\to$$ R be defined by $$f(x) = {{{x^2} - 3x - 6} \over {{x^2} + 2x + 4}}$$
Then which of the following statements is (are) TRUE?
Then which of the following statements is (are) TRUE?
f is decreasing in the interval ($$-$$2, $$-$$1)
f is increasing in the interval (1, 2)
f is onto
Range of f is $$\left[ { - {3 \over 2},2} \right]$$
Explanation
Given,
$$f(x) = {{{x^2} - 3x - 6} \over {{x^2} + 2x + 4}}$$ .... (i)
$$ \Rightarrow f'(x) = {{({x^2} + 2x + 4)(2x - 3) - ({x^2} - 3x - 6)(2x + 2)} \over {{{({x^2} + 2x + 4)}^2}}}$$
$$ \Rightarrow f'(x) = {{5x(x + 4)} \over {{{({x^2} + 2x + 4)}^2}}}$$

Sign scheme for f'(x)
Here, f is decreasing in the interval ($$-$$2, $$-$$1) and f is increasing in the interval (1, 2).
Now, $$f( - 4) = {{11} \over 6},f(0) = {{ - 3} \over 2}$$ [from Eq. (i)]
and $$\mathop {\lim }\limits_{x \to \pm \,\infty } f(x) = 1$$
$$\therefore$$ Range $$ = \left[ {{{ - 3} \over 2},{{11} \over 6}} \right]$$
Hence, f(x) is into.
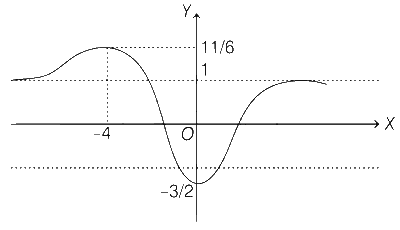
f(x) has local maxima at x = $$-$$4
and local minima at x = 0.
$$f(x) = {{{x^2} - 3x - 6} \over {{x^2} + 2x + 4}}$$ .... (i)
$$ \Rightarrow f'(x) = {{({x^2} + 2x + 4)(2x - 3) - ({x^2} - 3x - 6)(2x + 2)} \over {{{({x^2} + 2x + 4)}^2}}}$$
$$ \Rightarrow f'(x) = {{5x(x + 4)} \over {{{({x^2} + 2x + 4)}^2}}}$$

Sign scheme for f'(x)
Here, f is decreasing in the interval ($$-$$2, $$-$$1) and f is increasing in the interval (1, 2).
Now, $$f( - 4) = {{11} \over 6},f(0) = {{ - 3} \over 2}$$ [from Eq. (i)]
and $$\mathop {\lim }\limits_{x \to \pm \,\infty } f(x) = 1$$
$$\therefore$$ Range $$ = \left[ {{{ - 3} \over 2},{{11} \over 6}} \right]$$
Hence, f(x) is into.

f(x) has local maxima at x = $$-$$4
and local minima at x = 0.
Comments (0)


