JEE Advance - Mathematics (2021 - Paper 1 Online - No. 1)
Consider a triangle $$\Delta$$ whose two sides lie on the x-axis and the line x + y + 1 = 0. If the orthocenter of $$\Delta$$ is (1, 1), then the equation of the circle passing through the vertices of the triangle $$\Delta$$ is
x2 + y2 $$-$$ 3x + y = 0
x2 + y2 + x + 3y = 0
x2 + y2 + 2y $$-$$ 1 = 0
x2 + y2 + x + y = 0
Explanation
Equation of circle passing through C(0, 0) is
x2 + y2 + 2gx + 2fy = 0 ..... (i)
Since Eq. (i), also passes through ($$-$$1, 0) and (1, $$-$$2).
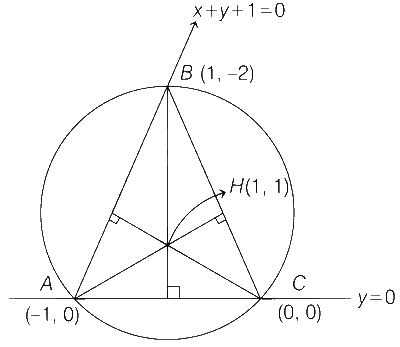
Then, 1 $$-$$ 2g = 0 $$\Rightarrow$$ g = 1 / 2
and 5 + 1 $$-$$ 4f = 0 $$\Rightarrow$$ f = 3 / 2
$$\therefore$$ Equation of circumcircle is x2 + y2 + 2 $$\times$$ $${1 \over 2}$$x + 2 $$\times$$ $${3 \over 2}$$y = 0
i.e. x2 + y2 + x + 3y = 0
x2 + y2 + 2gx + 2fy = 0 ..... (i)
Since Eq. (i), also passes through ($$-$$1, 0) and (1, $$-$$2).

Then, 1 $$-$$ 2g = 0 $$\Rightarrow$$ g = 1 / 2
and 5 + 1 $$-$$ 4f = 0 $$\Rightarrow$$ f = 3 / 2
$$\therefore$$ Equation of circumcircle is x2 + y2 + 2 $$\times$$ $${1 \over 2}$$x + 2 $$\times$$ $${3 \over 2}$$y = 0
i.e. x2 + y2 + x + 3y = 0
Comments (0)


