JEE Advance - Mathematics (2020 - Paper 2 Offline - No. 8)
Let a and b be positive real numbers such that a > 1 and b < a. Let P be a point in the first quadrant that lies on the hyperbola $${{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1$$. Suppose the tangent to the hyperbola at P passes through the point (1, 0), and suppose the normal to the hyperbola at P cuts off equal intercepts on the coordinate axes. Let $$\Delta $$ denote the area of the triangle formed by the tangent at P, the normal at P and the X-axis. If e denotes the eccentricity of the hyperbola, then which of the following statements is/are TRUE?
$$1 < e < \sqrt 2 $$
$$\sqrt 2 < e < 2$$
$$\Delta = {a^4}$$
$$\Delta = {b^4}$$
Explanation
Equation of given hyperbola is
$${{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1$$, a > b and a > 1
Let point P(a sec$$\theta $$, b tan$$\theta $$) on the hyperbola in first quadrant i.e., $$Qe\left( {0,{\pi \over 2}} \right)$$.
Now equation of tangent to the hyperbola at point P is
$${{x\sec \theta } \over a} - {{y\tan \theta } \over b} = 1$$ .... (i)
$$ \because $$ The tangent (i) passes through point A(1, 0)
So, $$a = \sec \theta > 1$$. ....(ii)
and equation of normal to the hyperbola at point P having slope is $${{b\sec \theta } \over {a\tan \theta }}$$, as normal cuts off equal intercepts on the coordinate axes, so slope must be $$-$$1.
Therefore, $${{b\sec \theta } \over {a\tan \theta }}$$ = $$-$$1
$$ \Rightarrow $$ $$b = - \tan \theta $$ {from Eq. (ii)}
$$ \because $$ The eccentricity of hyperbola
$$e = \sqrt {1 + {{{b^2}} \over {{a^2}}}} = \sqrt {1 + {{\sin }^2}\theta } $$
$$ \therefore $$ $$1 < e < \sqrt 2 $$, as $$\theta \in \left( {0,{\pi \over 2}} \right)$$
And the area of required triangle is, which is isosceles is
$$\Delta = {1 \over 2}{(AP)^2} = {1 \over 2}[{(1 - {\sec ^2}\theta )^2} + {\tan ^4}\theta ]$$
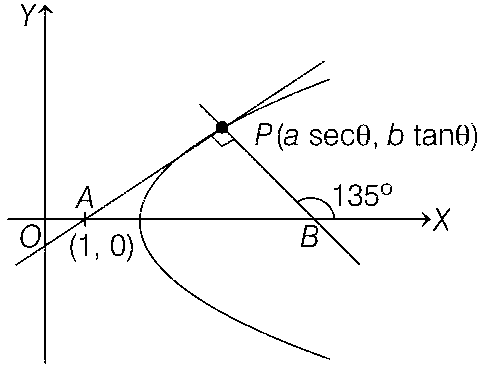
$$ = {1 \over 2}(2{\tan ^4}\theta ) = {\tan ^4}\theta = {b^4}$$.
$${{{x^2}} \over {{a^2}}} - {{{y^2}} \over {{b^2}}} = 1$$, a > b and a > 1
Let point P(a sec$$\theta $$, b tan$$\theta $$) on the hyperbola in first quadrant i.e., $$Qe\left( {0,{\pi \over 2}} \right)$$.
Now equation of tangent to the hyperbola at point P is
$${{x\sec \theta } \over a} - {{y\tan \theta } \over b} = 1$$ .... (i)
$$ \because $$ The tangent (i) passes through point A(1, 0)
So, $$a = \sec \theta > 1$$. ....(ii)
and equation of normal to the hyperbola at point P having slope is $${{b\sec \theta } \over {a\tan \theta }}$$, as normal cuts off equal intercepts on the coordinate axes, so slope must be $$-$$1.
Therefore, $${{b\sec \theta } \over {a\tan \theta }}$$ = $$-$$1
$$ \Rightarrow $$ $$b = - \tan \theta $$ {from Eq. (ii)}
$$ \because $$ The eccentricity of hyperbola
$$e = \sqrt {1 + {{{b^2}} \over {{a^2}}}} = \sqrt {1 + {{\sin }^2}\theta } $$
$$ \therefore $$ $$1 < e < \sqrt 2 $$, as $$\theta \in \left( {0,{\pi \over 2}} \right)$$
And the area of required triangle is, which is isosceles is
$$\Delta = {1 \over 2}{(AP)^2} = {1 \over 2}[{(1 - {\sec ^2}\theta )^2} + {\tan ^4}\theta ]$$

$$ = {1 \over 2}(2{\tan ^4}\theta ) = {\tan ^4}\theta = {b^4}$$.
Comments (0)


