JEE Advance - Mathematics (2020 - Paper 1 Offline - No. 3)
Let the functions f : R $$ \to $$ R and g : R $$ \to $$ R be defined by
f(x) = ex $$-$$ 1 $$-$$ e$$-$$|x $$-$$ 1|
and g(x) = $${1 \over 2}$$(ex $$-$$ 1 + e1 $$-$$ x).
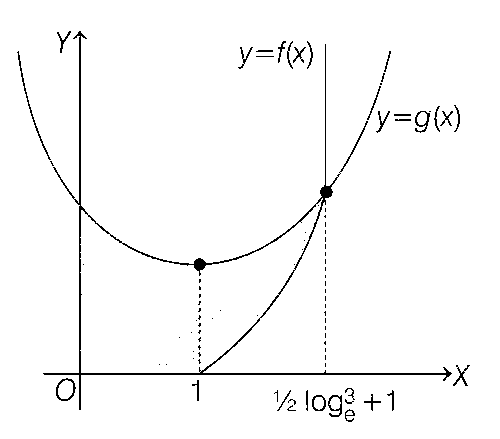
The the area of the region in the first quadrant bounded by the curves y = f(x), y = g(x) and x = 0 is
f(x) = ex $$-$$ 1 $$-$$ e$$-$$|x $$-$$ 1|
and g(x) = $${1 \over 2}$$(ex $$-$$ 1 + e1 $$-$$ x).
The the area of the region in the first quadrant bounded by the curves y = f(x), y = g(x) and x = 0 is
$$(2 - \sqrt 3 ) + {1 \over 2}(e - {e^{ - 1}})$$
$$(2 + \sqrt 3 ) + {1 \over 2}(e - {e^{ - 1}})$$
$$(2 - \sqrt 3 ) + {1 \over 2}(e + {e^{ - 1}})$$
$$(2 + \sqrt 3 ) + {1 \over 2}(e + {e^{ - 1}})$$
Explanation
The given functions f : R $$ \to $$ R and g : R $$ \to $$ R be defined by
$$f(x) = {e^{x - 1}} - {e^{ - |x - 1|}}$$
$$ = \left| \matrix{ {e^{x - 1}} - {e^{1 - x}},\,x\, \ge \,1 \hfill \cr 0,\,x < 1 \hfill \cr} \right.$$
and $$g(x) = {1 \over 2}({e^{x - 1}} + {e^{1 - x}})$$
For point of intersection of curves f(x) and g(x) put f(x) = g(x)
for $$x\, \ge \,1,\,{e^{x - 1}} - {e^{1 - x}} = {1 \over 2}({e^{x - 1}} + {e^{1 - x}})$$
$$ \Rightarrow {e^{x - 1}} = 3{e^{1 - x}} \Rightarrow {e^{2x}} = 3{e^2}$$
$$ \Rightarrow x = {1 \over 2}\log _e^3 + 1$$
So, required area is
$$\int_0^{1/2\log _e^3 + 1} {(g(x) - f(x))dx} $$
$$ = \int_0^{1/2\log _e^3 + 1} {g(x)dx - \int_1^{1/2\log _e^3 + 1} {f(x)dx} } $$
$$ = {1 \over 2}\int_0^{1/2\log _e^3 + 1} {({e^{x - 1}} + {e^{1 - x}})dx - } \int_1^{1/2\log _e^3 + 1} {({e^{x - 1}} - {e^{1 - x}})dx} $$
$$ = {1 \over 2}[{e^{x - 1}} - {e^{1 - x}}]_0^{{1 \over 2}\log _e^3 + 1} - [{e^{x - 1}} + {e^{1 - x}}]_1^{{1 \over 2}\log _e^3 + 1}$$
$$ = {1 \over 2}\left[ {\sqrt 3 - {1 \over {\sqrt 3 }} - {e^{ - 1}} + e} \right] - \left[ {\sqrt 3 + {1 \over {\sqrt 3 }} - 1 - 1} \right]$$
$$ = {1 \over {\sqrt 3 }} + {1 \over 2}(e - {e^{ - 1}}) - {4 \over {\sqrt 3 }} + 2$$
$$ = (2 - \sqrt 3 ) + {1 \over 2}(e - {e^{ - 1}})$$
$$f(x) = {e^{x - 1}} - {e^{ - |x - 1|}}$$
$$ = \left| \matrix{ {e^{x - 1}} - {e^{1 - x}},\,x\, \ge \,1 \hfill \cr 0,\,x < 1 \hfill \cr} \right.$$
and $$g(x) = {1 \over 2}({e^{x - 1}} + {e^{1 - x}})$$
For point of intersection of curves f(x) and g(x) put f(x) = g(x)
for $$x\, \ge \,1,\,{e^{x - 1}} - {e^{1 - x}} = {1 \over 2}({e^{x - 1}} + {e^{1 - x}})$$
$$ \Rightarrow {e^{x - 1}} = 3{e^{1 - x}} \Rightarrow {e^{2x}} = 3{e^2}$$
$$ \Rightarrow x = {1 \over 2}\log _e^3 + 1$$
So, required area is
$$\int_0^{1/2\log _e^3 + 1} {(g(x) - f(x))dx} $$
$$ = \int_0^{1/2\log _e^3 + 1} {g(x)dx - \int_1^{1/2\log _e^3 + 1} {f(x)dx} } $$
$$ = {1 \over 2}\int_0^{1/2\log _e^3 + 1} {({e^{x - 1}} + {e^{1 - x}})dx - } \int_1^{1/2\log _e^3 + 1} {({e^{x - 1}} - {e^{1 - x}})dx} $$

$$ = {1 \over 2}[{e^{x - 1}} - {e^{1 - x}}]_0^{{1 \over 2}\log _e^3 + 1} - [{e^{x - 1}} + {e^{1 - x}}]_1^{{1 \over 2}\log _e^3 + 1}$$
$$ = {1 \over 2}\left[ {\sqrt 3 - {1 \over {\sqrt 3 }} - {e^{ - 1}} + e} \right] - \left[ {\sqrt 3 + {1 \over {\sqrt 3 }} - 1 - 1} \right]$$
$$ = {1 \over {\sqrt 3 }} + {1 \over 2}(e - {e^{ - 1}}) - {4 \over {\sqrt 3 }} + 2$$
$$ = (2 - \sqrt 3 ) + {1 \over 2}(e - {e^{ - 1}})$$
Comments (0)


