JEE Advance - Mathematics (2020 - Paper 1 Offline - No. 10)
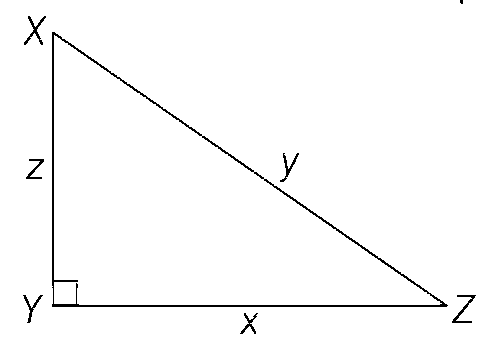
Let x, y and z be positive real numbers. Suppose x, y and z are the lengths of the sides of a triangle opposite to its angles X, Y, and Z, respectively. If
$$\tan {X \over 2} + \tan {Z \over 2} = {{2y} \over {x + y + z}}$$, then which of the following statements is/are TRUE?
$$\tan {X \over 2} + \tan {Z \over 2} = {{2y} \over {x + y + z}}$$, then which of the following statements is/are TRUE?
2Y = X + Z
Y = X + Z
$$\tan {X \over 2}$$ = $${x \over {y + z}}$$
x2 + z2 $$-$$ y2 = xz
Explanation
For a $$\Delta $$XYZ, it is given that
$$\tan {X \over 2} + \tan {Z \over 2} = {{2y} \over {x + y + z}}$$
$$ \Rightarrow {\Delta \over {s(s - x)}} + {\Delta \over {s(s - z)}} = {y \over s}$$
$$ \Rightarrow \Delta {{(s - z + s - x)} \over {(s - x)(s - z)}} = y$$
$$ \Rightarrow \Delta = (s - x)(s - z)$$
$$ \Rightarrow s(s - x)(s - y)(s - z) = {(s - x)^2}{(s - z)^2}$$
$$ \Rightarrow {s^2} - sy = {s^2} - (x + z)s + xz$$
$$ \Rightarrow s(x + z - y) = xz$$
$$ \Rightarrow {(x + z)^2} - {y^2} = 2xz$$
$$ \Rightarrow {x^2} + {z^2} = {y^2} \Rightarrow y = {\pi \over 2}$$
$$ \because $$ $$X + Y + Z = \pi \Rightarrow X + Z = {\pi \over 2} = Y$$
$$ \Rightarrow X + Z = Y$$
$$ \because $$ $$\tan {X \over 2} = \sqrt {{{1 - \cos x} \over {1 + \cos x}}} = \sqrt {{{1 - {z \over y}} \over {1 + {z \over y}}}} $$
$$ = \sqrt {{{y - z} \over {y + z}}} = {{\sqrt {{y^2} - {z^2}} } \over {y + z}}$$
$$\tan {X \over 2} = {x \over {y + z}}$$ {$$ \because $$ x2 + z2 = y2}
$$\tan {X \over 2} + \tan {Z \over 2} = {{2y} \over {x + y + z}}$$
$$ \Rightarrow {\Delta \over {s(s - x)}} + {\Delta \over {s(s - z)}} = {y \over s}$$
$$ \Rightarrow \Delta {{(s - z + s - x)} \over {(s - x)(s - z)}} = y$$
$$ \Rightarrow \Delta = (s - x)(s - z)$$
$$ \Rightarrow s(s - x)(s - y)(s - z) = {(s - x)^2}{(s - z)^2}$$
$$ \Rightarrow {s^2} - sy = {s^2} - (x + z)s + xz$$
$$ \Rightarrow s(x + z - y) = xz$$
$$ \Rightarrow {(x + z)^2} - {y^2} = 2xz$$
$$ \Rightarrow {x^2} + {z^2} = {y^2} \Rightarrow y = {\pi \over 2}$$
$$ \because $$ $$X + Y + Z = \pi \Rightarrow X + Z = {\pi \over 2} = Y$$
$$ \Rightarrow X + Z = Y$$
$$ \because $$ $$\tan {X \over 2} = \sqrt {{{1 - \cos x} \over {1 + \cos x}}} = \sqrt {{{1 - {z \over y}} \over {1 + {z \over y}}}} $$

$$ = \sqrt {{{y - z} \over {y + z}}} = {{\sqrt {{y^2} - {z^2}} } \over {y + z}}$$
$$\tan {X \over 2} = {x \over {y + z}}$$ {$$ \because $$ x2 + z2 = y2}
Comments (0)


