JEE Advance - Mathematics (2019 - Paper 2 Offline - No. 2)
Let f : R $$ \to $$ R be given by
$$f(x) = (x - 1)(x - 2)(x - 5)$$. Define
$$F(x) = \int\limits_0^x {f(t)dt} $$, x > 0
Then which of the following options is/are correct?
$$f(x) = (x - 1)(x - 2)(x - 5)$$. Define
$$F(x) = \int\limits_0^x {f(t)dt} $$, x > 0
Then which of the following options is/are correct?
F(x) $$ \ne $$ 0 for all x $$ \in $$ (0, 5)
F has a local maximum at x = 2
F has two local maxima and one local minimum in (0, $$\infty $$)
F has a local minimum at x = 1
Explanation
Given, f : R $$ \to $$ and
f(x) = (x $$-$$ 1)(x $$-$$ 2)(x $$-$$ 5)
Since, $$F(x) = \int_0^x {f(t)dt} $$, x > 0
So, $$F'(x) = f(x) = (x - 1)(x - 2)(x - 5)$$
According to wavy curve method
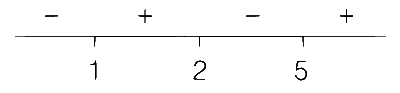
F'(x) changes, it's sign from negative to positive at x = 1 and 5, so F(x) has minima at x = 1 and 5 and as F'(x) changes, it's sign from positive to negative at x = 2, so F(x) has maxima at x = 2.
$$ \because $$ $$F'(2) = \int\limits_0^2 {f(t)dt = \int\limits_0^2 {({t^3} - 8{t^2}} } + 17t - 10)dt$$
$$ = \left[ {{{{t^4}} \over 4} - 8{{{t^3}} \over 3} + 17{{{t^2}} \over 2} - 10t} \right]_0^2$$
$$ = 4 - {{64} \over 3} + 34 - 20 = 38 - {{124} \over 3} = - {{10} \over 3}$$
$$ \because $$ AT the point of maxima x = 2, the functional value F(2), = $$ - {{10} \over 3}$$, is negative for the interval, x $$ \in $$(0, 5), so F(x) $$ \ne $$ 0 for any value of x $$ \in $$(0, 5),
Hence, options (a), (b) and (d) are correct.
f(x) = (x $$-$$ 1)(x $$-$$ 2)(x $$-$$ 5)
Since, $$F(x) = \int_0^x {f(t)dt} $$, x > 0
So, $$F'(x) = f(x) = (x - 1)(x - 2)(x - 5)$$
According to wavy curve method
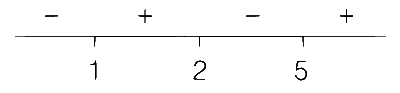
F'(x) changes, it's sign from negative to positive at x = 1 and 5, so F(x) has minima at x = 1 and 5 and as F'(x) changes, it's sign from positive to negative at x = 2, so F(x) has maxima at x = 2.
$$ \because $$ $$F'(2) = \int\limits_0^2 {f(t)dt = \int\limits_0^2 {({t^3} - 8{t^2}} } + 17t - 10)dt$$
$$ = \left[ {{{{t^4}} \over 4} - 8{{{t^3}} \over 3} + 17{{{t^2}} \over 2} - 10t} \right]_0^2$$
$$ = 4 - {{64} \over 3} + 34 - 20 = 38 - {{124} \over 3} = - {{10} \over 3}$$
$$ \because $$ AT the point of maxima x = 2, the functional value F(2), = $$ - {{10} \over 3}$$, is negative for the interval, x $$ \in $$(0, 5), so F(x) $$ \ne $$ 0 for any value of x $$ \in $$(0, 5),
Hence, options (a), (b) and (d) are correct.
Comments (0)


