JEE Advance - Mathematics (2019 - Paper 1 Offline - No. 6)
Define the collections {E1, E2, E3, ...} of ellipses and {R1, R2, R3.....} of rectangles as follows :
$${E_1}:{{{x^2}} \over 9} + {{{y^2}} \over 4} = 1$$
R1 : rectangle of largest area, with sides parallel to the axes, inscribed in E1;
En : ellipse $${{{x^2}} \over {a_n^2}} + {{{y^2}} \over {b_n^2}} = 1$$ of the largest area inscribed in $${R_{n - 1}},n > 1$$;
Rn : rectangle of largest area, with sides parallel to the axes, inscribed in En, n > 1.
Then which of the following options is/are correct?
$${E_1}:{{{x^2}} \over 9} + {{{y^2}} \over 4} = 1$$
R1 : rectangle of largest area, with sides parallel to the axes, inscribed in E1;
En : ellipse $${{{x^2}} \over {a_n^2}} + {{{y^2}} \over {b_n^2}} = 1$$ of the largest area inscribed in $${R_{n - 1}},n > 1$$;
Rn : rectangle of largest area, with sides parallel to the axes, inscribed in En, n > 1.
Then which of the following options is/are correct?
The eccentricities of E18 and E19 are not equal.
The distance of a focus from the centre in E9 is $${{\sqrt 5 } \over {32}}$$.
$$\sum\limits_{n = 1}^N {(area\,of\,{R_n})} $$ < 24, for each positive integer N.
The length of latusrectum of E9 is $${1 \over 6}$$
Explanation
Given equation of ellipse
$${E_1}:{{{x^2}} \over 9} + {{{y^2}} \over 4} = 1$$ ... (i)
Now, let a vertex of rectangle of largest area with sides parallel to the axes, inscribed in E1 be (3cos$$\theta $$, 2sin$$\theta $$).
So, area of rectangle
R1 = 2(3cos$$\theta $$) $$ \times $$ 2(2sin$$\theta $$) = 12sin(2$$\theta $$)
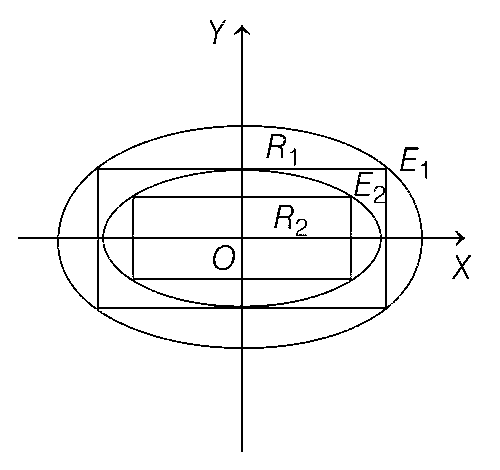
The area of R1 will be maximum, $$\theta = {\pi \over 4}$$ and maximum area is 12 square units and length of sides of rectangle R1 are $$2a\cos \theta = \sqrt 2 a = 3\sqrt 2 $$ = length of major axis of ellipse E2 and
$$2b\sin \theta = \sqrt 2 b = 2\sqrt 2 $$ = length of minor axis of ellipse E2.
So, $${E_2}:{{{x^2}} \over {{{\left( {{a \over {\sqrt 2 }}} \right)}^2}}} + {{{y^2}} \over {{{\left( {{b \over {\sqrt 2 }}} \right)}^2}}} = 1$$ and
maximum area of rectangle
$${R_2}:2\left( {{a \over {\sqrt 2 }}} \right)\left( {{b \over {\sqrt 2 }}} \right)$$ and so on.
So, $${E_n} = {{{x^2}} \over {{{\left( {{a \over {{{(\sqrt 2 )}^{n - 1}}}}} \right)}^2}}} + {{{y^2}} \over {{{\left( {{b \over {{{(\sqrt 2 )}^{n - 1}}}}} \right)}^2}}} = 1$$,
and maximum area of rectangle
$${R_n} = 2\left( {{a \over {{{(\sqrt 2 )}^{n - 1}}}}} \right) + \left( {{b \over {{{(\sqrt 2 )}^{n - 1}}}}} \right)$$
Now option (a),
Since, eccentricity of ellipse
$${E_n} = e{'_n} = \sqrt {1 - {{{{({b_n})}^2}} \over {{{({a_n})}^2}}}} $$
$$ = \sqrt {1 - {{{{\left( {{b \over {(\sqrt {2{)^{n - 1}}} }}} \right)}^2}} \over {{{\left( {{a \over {(\sqrt {2{)^{n - 1}}} }}} \right)}^2}}}} $$
$$ = \sqrt {1 - {{{b^2}} \over {{a^2}}}} = \sqrt {1 - {4 \over 9}} = {{\sqrt 5 } \over 3}$$
is independent of 'n', so eccentricity of E18 and E19 are equal.
Option (b),
Distance between focus and centre of
$${E_9} = e.{a_9} = {a \over {{{(\sqrt 2 )}^8}}}(e)$$
$$ = {3 \over {{2^4}}} \times {{\sqrt 5 } \over 3} = {{\sqrt 5 } \over {16}}$$ unit
Option (c),
$$ \because $$ $$\sum\limits_{n = 1}^N {(area\,of\,{R_n})} < (area\,of\,{R_1}) + (area\,of\,{R_2}) + .....\infty $$
$$ < 2ab + 2{{ab} \over 2} + 2{{ab} \over {{2^2}}} + .......$$
$$ < 2ab\left( {1 + {1 \over 2} + {1 \over {{2^2}}} + .....} \right)$$
$$ < 12\left( {{1 \over {1 - 1/2}}} \right)$$
$$ \Rightarrow \sum\limits_{n = 1}^N {(area\,of\,{R_n}} ) < 24$$, for each positive integer N.
Option (d),
Length of latusrectum $${E_9} = {{2b_9^2} \over {{a_9}}} = {{2{b^2}} \over {a{{(\sqrt 2 )}^8}}}$$
$$ = {{2 \times 4} \over {3 \times 16}} = {1 \over 6}$$ units
Hence, options (c) and (d) are correct.
$${E_1}:{{{x^2}} \over 9} + {{{y^2}} \over 4} = 1$$ ... (i)
Now, let a vertex of rectangle of largest area with sides parallel to the axes, inscribed in E1 be (3cos$$\theta $$, 2sin$$\theta $$).
So, area of rectangle
R1 = 2(3cos$$\theta $$) $$ \times $$ 2(2sin$$\theta $$) = 12sin(2$$\theta $$)

The area of R1 will be maximum, $$\theta = {\pi \over 4}$$ and maximum area is 12 square units and length of sides of rectangle R1 are $$2a\cos \theta = \sqrt 2 a = 3\sqrt 2 $$ = length of major axis of ellipse E2 and
$$2b\sin \theta = \sqrt 2 b = 2\sqrt 2 $$ = length of minor axis of ellipse E2.
So, $${E_2}:{{{x^2}} \over {{{\left( {{a \over {\sqrt 2 }}} \right)}^2}}} + {{{y^2}} \over {{{\left( {{b \over {\sqrt 2 }}} \right)}^2}}} = 1$$ and
maximum area of rectangle
$${R_2}:2\left( {{a \over {\sqrt 2 }}} \right)\left( {{b \over {\sqrt 2 }}} \right)$$ and so on.
So, $${E_n} = {{{x^2}} \over {{{\left( {{a \over {{{(\sqrt 2 )}^{n - 1}}}}} \right)}^2}}} + {{{y^2}} \over {{{\left( {{b \over {{{(\sqrt 2 )}^{n - 1}}}}} \right)}^2}}} = 1$$,
and maximum area of rectangle
$${R_n} = 2\left( {{a \over {{{(\sqrt 2 )}^{n - 1}}}}} \right) + \left( {{b \over {{{(\sqrt 2 )}^{n - 1}}}}} \right)$$
Now option (a),
Since, eccentricity of ellipse
$${E_n} = e{'_n} = \sqrt {1 - {{{{({b_n})}^2}} \over {{{({a_n})}^2}}}} $$
$$ = \sqrt {1 - {{{{\left( {{b \over {(\sqrt {2{)^{n - 1}}} }}} \right)}^2}} \over {{{\left( {{a \over {(\sqrt {2{)^{n - 1}}} }}} \right)}^2}}}} $$
$$ = \sqrt {1 - {{{b^2}} \over {{a^2}}}} = \sqrt {1 - {4 \over 9}} = {{\sqrt 5 } \over 3}$$
is independent of 'n', so eccentricity of E18 and E19 are equal.
Option (b),
Distance between focus and centre of
$${E_9} = e.{a_9} = {a \over {{{(\sqrt 2 )}^8}}}(e)$$
$$ = {3 \over {{2^4}}} \times {{\sqrt 5 } \over 3} = {{\sqrt 5 } \over {16}}$$ unit
Option (c),
$$ \because $$ $$\sum\limits_{n = 1}^N {(area\,of\,{R_n})} < (area\,of\,{R_1}) + (area\,of\,{R_2}) + .....\infty $$
$$ < 2ab + 2{{ab} \over 2} + 2{{ab} \over {{2^2}}} + .......$$
$$ < 2ab\left( {1 + {1 \over 2} + {1 \over {{2^2}}} + .....} \right)$$
$$ < 12\left( {{1 \over {1 - 1/2}}} \right)$$
$$ \Rightarrow \sum\limits_{n = 1}^N {(area\,of\,{R_n}} ) < 24$$, for each positive integer N.
Option (d),
Length of latusrectum $${E_9} = {{2b_9^2} \over {{a_9}}} = {{2{b^2}} \over {a{{(\sqrt 2 )}^8}}}$$
$$ = {{2 \times 4} \over {3 \times 16}} = {1 \over 6}$$ units
Hence, options (c) and (d) are correct.
Comments (0)


