JEE Advance - Mathematics (2019 - Paper 1 Offline - No. 14)
Let the point B be the reflection of the point A(2, 3) with respect to the line $$8x - 6y - 23 = 0$$. Let $$\Gamma_{A} $$ and $$\Gamma_{B} $$ be circles of radii 2 and 1 with centres A and B respectively. Let T be a common tangent to the circles $$\Gamma_{A} $$ and $$\Gamma_{B} $$ such that both the circles are on the same side of T. If C is the point of intersection of T and the line passing through A and B, then the length of the line segment AC is .................
Answer
10
Explanation
According to given information the figure is as following
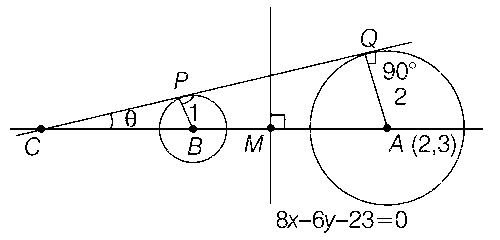
From the figure,
$$AC = {2 \over {\sin \theta }}$$ ....(i)
$$ \because $$ $$\sin \theta = {1 \over {CB}}$$ (from $$\Delta $$CPB) .... (ii)
and $$\sin \theta = {2 \over {AC}} = {2 \over {CB + AB}}$$ (from $$\Delta $$CQA) ....(iii)
$$ \because $$ AB = AM + MB = 2AM [$$ \because $$ AM = MB]
$$ = 2{{\left| {(8 \times 2) - (6 \times 3) - 23} \right|} \over {\sqrt {64 + 36} }}$$
$$ = {{2 \times 25} \over {10}} = 5.00$$
From Eqs. (ii) and (iii), we get
$$\sin \theta = {1 \over {CB}} = {2 \over {CB + AB}}$$
$$ \Rightarrow {1 \over {CB}} = {2 \over {CB + 5}}$$ [$$ \because $$ AB = 5]
$$ \Rightarrow CB + 5 = 2CB \Rightarrow CB = 5 = {1 \over {\sin \theta }}$$
From the Eq. (i), we get
$$AC = {2 \over {\sin \theta }} = 2 \times 5 = 10.00$$

From the figure,
$$AC = {2 \over {\sin \theta }}$$ ....(i)
$$ \because $$ $$\sin \theta = {1 \over {CB}}$$ (from $$\Delta $$CPB) .... (ii)
and $$\sin \theta = {2 \over {AC}} = {2 \over {CB + AB}}$$ (from $$\Delta $$CQA) ....(iii)
$$ \because $$ AB = AM + MB = 2AM [$$ \because $$ AM = MB]
$$ = 2{{\left| {(8 \times 2) - (6 \times 3) - 23} \right|} \over {\sqrt {64 + 36} }}$$
$$ = {{2 \times 25} \over {10}} = 5.00$$
From Eqs. (ii) and (iii), we get
$$\sin \theta = {1 \over {CB}} = {2 \over {CB + AB}}$$
$$ \Rightarrow {1 \over {CB}} = {2 \over {CB + 5}}$$ [$$ \because $$ AB = 5]
$$ \Rightarrow CB + 5 = 2CB \Rightarrow CB = 5 = {1 \over {\sin \theta }}$$
From the Eq. (i), we get
$$AC = {2 \over {\sin \theta }} = 2 \times 5 = 10.00$$
Comments (0)


