Given,

$$\mathop {\lim }\limits_{t \to x} {{f(x)\sin t - f(t)\sin x} \over {t - x}} = {\sin ^2}x$$

Using L' Hospital rules

$$\mathop {\lim }\limits_{t \to x} {{f(x)\cos t - f'(t)\sin x} \over 1} = {\sin ^2}x$$

$$ \Rightarrow f(x)\cos x - f'(x)\sin x = {\sin ^2}x$$

$$ \Rightarrow f'(x)\sin x - f(x)\cos x = - {\sin ^2}x$$

$$ \Rightarrow {{f'(x)\sin x - f(x)\cos x} \over {{{\sin }^2}x}} = - 1$$

$$ \Rightarrow d\left( {{{f(x)} \over {\sin x}}} \right) = - 1$$

On integrating, we get

$${{f(x)} \over {\sin x}} = - x + C$$

$$ \Rightarrow f(x) = - x\sin x + C\sin x$$

It is given that $$x = {\pi \over 6},\,f\left( {{\pi \over 6}} \right) = - {\pi \over {12}}$$

$$ \therefore $$ $$f\left( {{\pi \over 6}} \right) = - {\pi \over 6}\sin {\pi \over 6} + C\sin {\pi \over 6}$$

$$ = - {\pi \over {12}} = - {\pi \over {12}} + {1 \over 2}C$$

$$ \Rightarrow C = 0$$

$$ \therefore $$ $$f(x) = - x\sin x$$

(a) $$f(x) = - x\sin x$$

$$f\left( {{\pi \over 4}} \right) = - {\pi \over 4}\sin {\pi \over 4} = - {\pi \over {4\sqrt 2 }}$$ false

(b) f(x) = $$-$$ x sin x

$$\sin x > x - {{{x^3}} \over 6},\,\forall x \in (0,\pi )$$

$$ \Rightarrow - x\sin x < - {x^2} + {{{x^4}} \over 6}$$

$$ \Rightarrow f(x) < {{{x^4}} \over 6} - {x^2},\,\forall x \in (0,\,\pi )$$

It is true.

(c) f(x) = $$-$$x sin x

f'(x) = $$-$$ sin x $$-$$ x cos x

f'(x) = 0

$$ \Rightarrow $$ $$-$$ sin x $$-$$ x cos x = 0

tan x = $$-$$ x



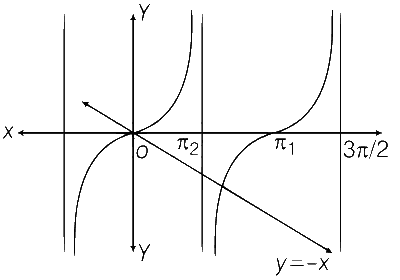
$$ \Rightarrow $$ Their exists $$\alpha $$$$ \in $$(0, $$\pi $$) for which f'($$\alpha $$) = 0

It is true.

(d) $$f(x) = - x\sin x$$

$$f'(x) = - \sin x - x\cos x$$

$$f''(x) = - 2\cos x + x\sin x$$

$$f''\left( {{\pi \over 2}} \right) = {\pi \over 2},\,f\left( {{\pi \over 2}} \right) = - {\pi \over 2}$$

$$ \therefore $$ $$f''\left( {{\pi \over 2}} \right) + f\left( {{\pi \over 2}} \right) = 0$$

It is true.