JEE Advance - Mathematics (2018 - Paper 2 Offline - No. 4)
Consider two straight lines, each of which is tangent to both the circle x2 + y2 = (1/2) and the parabola y2 = 4x. Let these lines intersect at the point Q. Consider the ellipse whose centre is at the origin O(0, 0) and whose semi-major axis is OQ. If the length of the minor axis of this ellipse is $$\sqrt 2 $$, then which of the following statement(s) is (are) TRUE?
For the ellipse, the eccentricity is 1$$\sqrt 2 $$ and the length of the latus rectum is 1
For the ellipse, the eccentricity is 1/2 and the length of the latus rectum is 1/2
The area of the region bounded by the ellipse between the lines $$x = {1 \over {\sqrt 2 }}$$ and x = 1 is $${1 \over {4\sqrt 2 }}(\pi - 2)$$
The area of the region bounded by the ellipse between the lines $$x = {1 \over {\sqrt 2 }}$$ and x = 1 is $${1 \over {16}}(\pi - 2)$$
Explanation
We have,
Equations of circle
$${x^2} + {y^2} = {1 \over 2}$$
and Equations of parabola
y2 = 4x
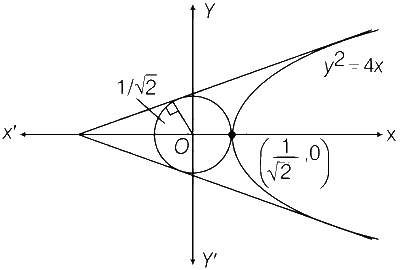
Let the equation of common tangent of parabola and circle is
$$y = mx + {1 \over m}$$
Since, radius of circle = $${1 \over {\sqrt 2 }}$$
$$ \therefore $$ $${1 \over {\sqrt 2 }}$$ = $$\left| {{{0 + 0 + {1 \over m}} \over {\sqrt {1 + {m^2}} }}} \right|$$
$$ \Rightarrow $$ m4 + m2 $$-$$ 2 = 0
$$ \Rightarrow $$ m =$$ \pm $$1
$$ \therefore $$ Equation of common tangents are
y = x + 1 and y = $$-$$x$$-$$1
Intersection point of common tangent at Q($$-$$1, 0)
$$ \therefore $$ Equation of ellipse
$${{{x^2}} \over 1} + {{{y^2}} \over {1/2}} = 1$$
where, $${a^2} = 1$$, $${b^2} = 1/2$$
Now, eccentricity
$$ = \sqrt {1 - {{{b^2}} \over {{a^2}}}} = \sqrt {1 - {1 \over 2}} = {1 \over {\sqrt 2 }}$$
and length of latusrectum
$$ = {{2{b^2}} \over a} = {{2\left( {{1 \over 2}} \right)} \over 1} = 1$$
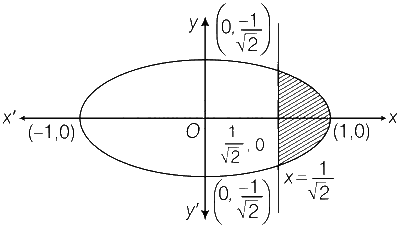
$$ \therefore $$ Area of shaded region
$$ = 2\int_{1/\sqrt 2 }^1 {{1 \over {\sqrt 2 }}} \sqrt {1 - {x^2}} dx$$
$$\eqalign{ & = \sqrt 2 \left[ {{x \over 2}\sqrt {1 - {x^2}} + {1 \over 2}{{\sin }^{ - 1}}x} \right]_{1/\sqrt 2 }^1 \cr & = \sqrt 2 \left[ {\left( {0 + {\pi \over 4}} \right) - \left( {{1 \over 4} + {\pi \over 8}} \right)} \right] \cr} $$
$$ = \sqrt 2 \left[ {\left( {0 + {\pi \over 4}} \right) - \left( {{1 \over 4} + {\pi \over 8}} \right)} \right]$$
$$ = \sqrt 2 \left( {{\pi \over 8} - {1 \over 4}} \right) = {{\pi - 2} \over {4\sqrt 2 }}$$
Equations of circle
$${x^2} + {y^2} = {1 \over 2}$$
and Equations of parabola
y2 = 4x

Let the equation of common tangent of parabola and circle is
$$y = mx + {1 \over m}$$
Since, radius of circle = $${1 \over {\sqrt 2 }}$$
$$ \therefore $$ $${1 \over {\sqrt 2 }}$$ = $$\left| {{{0 + 0 + {1 \over m}} \over {\sqrt {1 + {m^2}} }}} \right|$$
$$ \Rightarrow $$ m4 + m2 $$-$$ 2 = 0
$$ \Rightarrow $$ m =$$ \pm $$1
$$ \therefore $$ Equation of common tangents are
y = x + 1 and y = $$-$$x$$-$$1
Intersection point of common tangent at Q($$-$$1, 0)
$$ \therefore $$ Equation of ellipse
$${{{x^2}} \over 1} + {{{y^2}} \over {1/2}} = 1$$
where, $${a^2} = 1$$, $${b^2} = 1/2$$
Now, eccentricity
$$ = \sqrt {1 - {{{b^2}} \over {{a^2}}}} = \sqrt {1 - {1 \over 2}} = {1 \over {\sqrt 2 }}$$
and length of latusrectum
$$ = {{2{b^2}} \over a} = {{2\left( {{1 \over 2}} \right)} \over 1} = 1$$

$$ \therefore $$ Area of shaded region
$$ = 2\int_{1/\sqrt 2 }^1 {{1 \over {\sqrt 2 }}} \sqrt {1 - {x^2}} dx$$
$$\eqalign{ & = \sqrt 2 \left[ {{x \over 2}\sqrt {1 - {x^2}} + {1 \over 2}{{\sin }^{ - 1}}x} \right]_{1/\sqrt 2 }^1 \cr & = \sqrt 2 \left[ {\left( {0 + {\pi \over 4}} \right) - \left( {{1 \over 4} + {\pi \over 8}} \right)} \right] \cr} $$
$$ = \sqrt 2 \left[ {\left( {0 + {\pi \over 4}} \right) - \left( {{1 \over 4} + {\pi \over 8}} \right)} \right]$$
$$ = \sqrt 2 \left( {{\pi \over 8} - {1 \over 4}} \right) = {{\pi - 2} \over {4\sqrt 2 }}$$
Comments (0)


