JEE Advance - Mathematics (2018 - Paper 1 Offline - No. 2)
In a $$\Delta $$PQR = 30$$^\circ $$ and the sides PQ and QR have lengths 10$$\sqrt 3 $$ and 10, respectively. Then, which of the following statement(s) is(are) TRUE?
$$\angle QPR = 45^\circ $$
The area of the $$\Delta PQR$$ is $$25\sqrt 3 $$ and $$\angle QRP = 120^\circ $$
The radius of the incircle of the $$\Delta PQR$$ is $$10\sqrt 3 $$ $$-$$ 15
The area of the circumcircle of the $$\Delta PQR$$ is 100$$\pi $$
Explanation
We have,
In $$\Delta $$PQR
$$\angle PQR = 30^\circ $$
$$PQ = 10\sqrt 3 $$
$$QR = 10$$
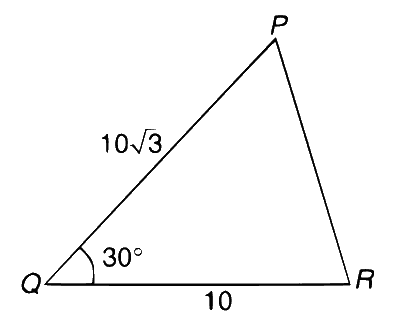
By cosine rule
$$\cos 30^\circ = {{P{Q^2} + Q{R^2} - P{R^2}} \over {2PQ.QR}}$$
$$ \Rightarrow {{\sqrt 3 } \over 2} = {{300 + 100 - P{R^2}} \over {200\sqrt 3 }}$$
$$ \Rightarrow 300 = 300 + 100 - P{R^2}$$
$$ \Rightarrow PR = 10$$
Since, $$PR = QR = 10$$
$$ \therefore $$ $$\angle QPR = 30^\circ $$ and $$\angle QRP = 120^\circ $$
Area of $$\Delta PQR = {1 \over 2}PQ.QR.\sin 30^\circ $$
$$ = {1 \over 2} \times 10\sqrt 3 \times 10 \times {1 \over 2} = 25\sqrt 3 $$
Radius of incircle of
$$\Delta PQR = {{Area\,of\,\Delta PQR} \over {Semi - perimetre\,of\,\Delta PQR}}$$
i.e. $$r = {\Delta \over s} = {{25\sqrt 3 } \over {{{10\sqrt 3 + 10 + 10} \over 2}}} = {{25\sqrt 3 } \over {5(\sqrt 3 + 2)}}$$
$$ \Rightarrow r = 5\sqrt 3 (2 - \sqrt 3 ) = 10\sqrt 3 - 15$$
and radius of circumcircle
$$(R) = {{abc} \over {4\Delta }} = {{10\sqrt 3 \times 10 \times 10} \over {4 \times 25\sqrt 3 }} = 10$$
$$ \therefore $$ Area of circumcircle of
$$\Delta PQR = \pi {R^2} = 100\pi $$
Hence, option (b), (c) and (d) are correct answer.
In $$\Delta $$PQR
$$\angle PQR = 30^\circ $$
$$PQ = 10\sqrt 3 $$
$$QR = 10$$

By cosine rule
$$\cos 30^\circ = {{P{Q^2} + Q{R^2} - P{R^2}} \over {2PQ.QR}}$$
$$ \Rightarrow {{\sqrt 3 } \over 2} = {{300 + 100 - P{R^2}} \over {200\sqrt 3 }}$$
$$ \Rightarrow 300 = 300 + 100 - P{R^2}$$
$$ \Rightarrow PR = 10$$
Since, $$PR = QR = 10$$
$$ \therefore $$ $$\angle QPR = 30^\circ $$ and $$\angle QRP = 120^\circ $$
Area of $$\Delta PQR = {1 \over 2}PQ.QR.\sin 30^\circ $$
$$ = {1 \over 2} \times 10\sqrt 3 \times 10 \times {1 \over 2} = 25\sqrt 3 $$
Radius of incircle of
$$\Delta PQR = {{Area\,of\,\Delta PQR} \over {Semi - perimetre\,of\,\Delta PQR}}$$
i.e. $$r = {\Delta \over s} = {{25\sqrt 3 } \over {{{10\sqrt 3 + 10 + 10} \over 2}}} = {{25\sqrt 3 } \over {5(\sqrt 3 + 2)}}$$
$$ \Rightarrow r = 5\sqrt 3 (2 - \sqrt 3 ) = 10\sqrt 3 - 15$$
and radius of circumcircle
$$(R) = {{abc} \over {4\Delta }} = {{10\sqrt 3 \times 10 \times 10} \over {4 \times 25\sqrt 3 }} = 10$$
$$ \therefore $$ Area of circumcircle of
$$\Delta PQR = \pi {R^2} = 100\pi $$
Hence, option (b), (c) and (d) are correct answer.
Comments (0)


