JEE Advance - Mathematics (2018 - Paper 1 Offline - No. 16)
Let S be the circle in the XY-plane defined the equation x2 + y2 = 4.
Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve
Let P be a point on the circle S with both coordinates being positive. Let the tangent to S at P intersect the coordinate axes at the points M and N. Then, the mid-point of the line segment MN must lie on the curve
(x + y)2 = 3xy
x2/3 + y2/3 = 24/3
x2 + y2 = 2xy
x2 + y2 = x2y2
Explanation
We have,
x2 + y2 = 4
Let P(2 cos$$\theta $$, 2 sin$$\theta $$) be a point on a circle.
$$ \therefore $$ Tangent at P is
2 cos$$\theta $$x + 2 sin$$\theta $$y = 4
$$ \Rightarrow $$ x cos$$\theta $$ + y sin$$\theta $$ = 2
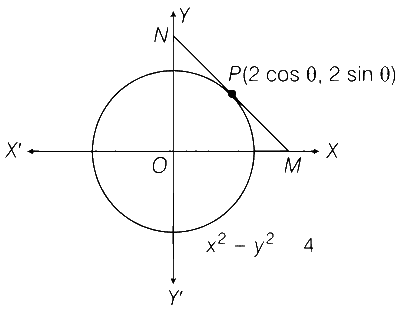
$$ \therefore $$ The coordinates at $$M\left( {{2 \over {\cos \theta }},0} \right)$$ and $$N\left( {0,{2 \over {\sin \theta }}} \right)$$
Let (h, k) is mid-point of MN
$$ \therefore $$ $$h = {1 \over {\cos \theta }}$$ and $$k = {1 \over {\sin \theta }}$$
$$ \Rightarrow $$ $$\cos \theta = {1 \over h}$$
and $$\sin \theta = {1 \over k}$$
$$ \Rightarrow $$ $${\cos ^2}\theta + {\sin ^2}\theta = {1 \over {{h^2}}} + {1 \over {{k^2}}}$$
$$ \Rightarrow 1 = {{{h^2} + {k^2}} \over {{h^2}.{k^2}}}$$
$${h^2} + {k^2} = {h^2}{k^2}$$
$$ \therefore $$ Mid-point of MN lie on the curve
$${x^2} + {y^2} = {x^2}{y^2}$$
x2 + y2 = 4
Let P(2 cos$$\theta $$, 2 sin$$\theta $$) be a point on a circle.
$$ \therefore $$ Tangent at P is
2 cos$$\theta $$x + 2 sin$$\theta $$y = 4
$$ \Rightarrow $$ x cos$$\theta $$ + y sin$$\theta $$ = 2

$$ \therefore $$ The coordinates at $$M\left( {{2 \over {\cos \theta }},0} \right)$$ and $$N\left( {0,{2 \over {\sin \theta }}} \right)$$
Let (h, k) is mid-point of MN
$$ \therefore $$ $$h = {1 \over {\cos \theta }}$$ and $$k = {1 \over {\sin \theta }}$$
$$ \Rightarrow $$ $$\cos \theta = {1 \over h}$$
and $$\sin \theta = {1 \over k}$$
$$ \Rightarrow $$ $${\cos ^2}\theta + {\sin ^2}\theta = {1 \over {{h^2}}} + {1 \over {{k^2}}}$$
$$ \Rightarrow 1 = {{{h^2} + {k^2}} \over {{h^2}.{k^2}}}$$
$${h^2} + {k^2} = {h^2}{k^2}$$
$$ \therefore $$ Mid-point of MN lie on the curve
$${x^2} + {y^2} = {x^2}{y^2}$$
Comments (0)


