JEE Advance - Mathematics (2018 - Paper 1 Offline - No. 1)
For a non-zero complex number z, let arg(z) denote the principal argument with $$-$$ $$\pi $$ < arg(z) $$ \le $$ $$\pi $$. Then, which of the following statement(s) is (are) FALSE?
arg($$-$$1$$-$$i) = $${\pi \over 4}$$, where i = $$\sqrt { - 1} $$
The function f : R $$ \to $$ ($$-$$$$\pi $$, $$\pi $$), defined by f(t) = arg ($$-$$1 + it) for all t $$ \in $$ R, is continuous at all points of R, where i = $$\sqrt { - 1} $$.
For any two non-zero complex numbers z1 and z2, arg $$\left( {{{{z_1}} \over {{z_2}}}} \right)$$$$-$$ arg (z1) + arg(z2) is an integer multiple of 2$$\pi $$.
For any three given distinct complex numbers z1, z2 and z3, the locus of the point z satisfying the condition arg$$\left( {{{(z - {z_1})({z_2} - {z_3})} \over {(z - {z_3})({z_2} - {z_1})}}} \right) = \pi $$, lies on a straight line.
Explanation
(a) Let z= $$-$$1$$-$$i and arg(z) = $$\theta $$
Now, $$\tan \theta = \left| {{{im(z)} \over {{\mathop{\rm Re}\nolimits} (z)}}} \right| = \left| {{{ - 1} \over { - 1}}} \right| = 1$$
$$ \Rightarrow $$ $$\theta = {\pi \over 4}$$
Since, x < 0, y < 0
$$ \therefore $$ $$\arg (z) = - \left( {\pi - {\pi \over 4}} \right) = - {{3\pi } \over 4}$$
(b) We have, f(t) = arg($$-$$1 + it)
$$\arg ( - 1 + it) = \left\{ \matrix{ \pi - {\tan ^{ - 1}}t,\,t \ge 0 \hfill \cr - (\pi + {\tan ^{ - 1}}t),\,t < 0 \hfill \cr} \right.$$
This function is discontinuous at t = 0.
(c) We have,
$$\arg \left( {{{{z_1}} \over {{z_2}}}} \right) = arg({z_1}) - arg({z_2}) + 2n\pi $$
$$ \therefore $$ $$\arg \left( {{{{z_1}} \over {{z_2}}}} \right) - arg({z_1}) + arg({z_2})$$
= arg(z1) $$-$$ arg(z2) + 2n$$\pi $$ $$-$$ arg(z1) + arg(z2) = 2n$$\pi $$
So, given expression is multiple of 2$$\pi $$.
(d) We have, $$\arg \left( {{{(z - {z_1})({z_2} - {z_3})} \over {(z - {z_3})({z_2} - {z_1})}}} \right) = \pi $$
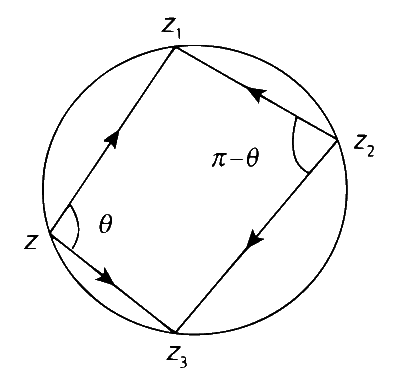
Now, $$\arg \left( {{{{z_1} - z} \over {{z_3} - z}}} \right) = \theta $$
and $$\arg \left( {{{{z_3} - {z_2}} \over {{z_1} - {z_2}}}} \right) = \pi - \theta $$
Therefore, $$\arg \left( {{{{z_1} - z} \over {{z_3} - z}}} \right) + \arg \left( {{{{z_3} - {z_2}} \over {{z_1} - {z_2}}}} \right) = \theta + \pi - \theta $$
That is,
$$\arg \left( {{{{z_1} - z} \over {{z_3} - z}}.{{{z_3} - {z_2}} \over {{z_1} - {z_2}}}} \right) = \arg \left( {{{\left( {{z_1} - z} \right)\left( {{z_3} - {z_2}} \right)} \over {\left( {{z_3} - z} \right)\left( {{z_1} - {z_2}} \right)}}} \right) = \pi $$
This implies that for any three given distinct complex numbers z1 , z2 and z3 , the locus of the point z satisfying the condition
$$\arg \left( {{{\left( {{z_1} - z} \right)\left( {{z_3} - {z_2}} \right)} \over {\left( {{z_3} - z} \right)\left( {{z_1} - {z_2}} \right)}}} \right) = \pi $$, lies on a circle.
$$ \therefore $$ (a), (b), (d) are false statement.
Hence, option (a), (b), (d) are correct answer.
Now, $$\tan \theta = \left| {{{im(z)} \over {{\mathop{\rm Re}\nolimits} (z)}}} \right| = \left| {{{ - 1} \over { - 1}}} \right| = 1$$
$$ \Rightarrow $$ $$\theta = {\pi \over 4}$$
Since, x < 0, y < 0
$$ \therefore $$ $$\arg (z) = - \left( {\pi - {\pi \over 4}} \right) = - {{3\pi } \over 4}$$
(b) We have, f(t) = arg($$-$$1 + it)
$$\arg ( - 1 + it) = \left\{ \matrix{ \pi - {\tan ^{ - 1}}t,\,t \ge 0 \hfill \cr - (\pi + {\tan ^{ - 1}}t),\,t < 0 \hfill \cr} \right.$$
This function is discontinuous at t = 0.
(c) We have,
$$\arg \left( {{{{z_1}} \over {{z_2}}}} \right) = arg({z_1}) - arg({z_2}) + 2n\pi $$
$$ \therefore $$ $$\arg \left( {{{{z_1}} \over {{z_2}}}} \right) - arg({z_1}) + arg({z_2})$$
= arg(z1) $$-$$ arg(z2) + 2n$$\pi $$ $$-$$ arg(z1) + arg(z2) = 2n$$\pi $$
So, given expression is multiple of 2$$\pi $$.
(d) We have, $$\arg \left( {{{(z - {z_1})({z_2} - {z_3})} \over {(z - {z_3})({z_2} - {z_1})}}} \right) = \pi $$

Now, $$\arg \left( {{{{z_1} - z} \over {{z_3} - z}}} \right) = \theta $$
and $$\arg \left( {{{{z_3} - {z_2}} \over {{z_1} - {z_2}}}} \right) = \pi - \theta $$
Therefore, $$\arg \left( {{{{z_1} - z} \over {{z_3} - z}}} \right) + \arg \left( {{{{z_3} - {z_2}} \over {{z_1} - {z_2}}}} \right) = \theta + \pi - \theta $$
That is,
$$\arg \left( {{{{z_1} - z} \over {{z_3} - z}}.{{{z_3} - {z_2}} \over {{z_1} - {z_2}}}} \right) = \arg \left( {{{\left( {{z_1} - z} \right)\left( {{z_3} - {z_2}} \right)} \over {\left( {{z_3} - z} \right)\left( {{z_1} - {z_2}} \right)}}} \right) = \pi $$
This implies that for any three given distinct complex numbers z1 , z2 and z3 , the locus of the point z satisfying the condition
$$\arg \left( {{{\left( {{z_1} - z} \right)\left( {{z_3} - {z_2}} \right)} \over {\left( {{z_3} - z} \right)\left( {{z_1} - {z_2}} \right)}}} \right) = \pi $$, lies on a circle.
$$ \therefore $$ (a), (b), (d) are false statement.
Hence, option (a), (b), (d) are correct answer.
Comments (0)


