Sign In

JEE Advance - Mathematics (2017 - Paper 2 Offline - No. 16)

Let O be the origin and $$\overrightarrow{OX}$$, $$\overrightarrow{OY}$$, $$\overrightarrow{OZ}$$ be three unit vectors in the directions of the sides $$\overrightarrow{QR}$$, $$\overrightarrow{RP}$$, $$\overrightarrow{PQ}$$ respectively, of a triangle PQR.
Let O be the origin and $$\overrightarrow{OX}$$, $$\overrightarrow{OY}$$, $$\overrightarrow{OZ}$$ be three unit vectors in the directions of the sides $$\overrightarrow{QR}$$, $$\overrightarrow{RP}$$, $$\overrightarrow{PQ}$$ respectively, of a triangle PQR.
Let O be the origin and $$\overrightarrow{OX}$$, $$\overrightarrow{OY}$$, $$\overrightarrow{OZ}$$ be three unit vectors in the directions of the sides $$\overrightarrow{QR}$$, $$\overrightarrow{RP}$$, $$\overrightarrow{PQ}$$ respectively, of a triangle PQR.
|$$\overrightarrow{OX}$$ $$ \times $$ $$\overrightarrow{OY}$$| = ?
sin(P + Q)
sin(P + R)
sin(Q + R)
sin2R

Explanation

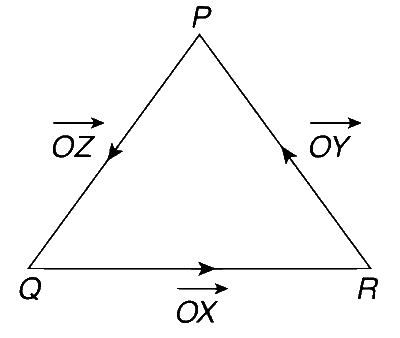
JEE Advanced 2017 Paper 2 Offline Mathematics - Vector Algebra Question 10 English Explanation

Now, $$\overrightarrow {OX} = {{\overrightarrow {QR} } \over {QR}}$$

and $$\overrightarrow {OY} = {{\overrightarrow {RP} } \over {RP}}$$

Therefore, $$(\overrightarrow {OX} \times \overrightarrow {OY} ) = {{\overrightarrow {QR} } \over {QR}} \times {{\overrightarrow {RP} } \over {RP}} = {{\overrightarrow {QR} \times \overrightarrow {RP} } \over {PQ}}$$

$$ = {{PQ\sin R} \over {PQ}} = \sin R = \sin (\pi - (P + Q) = \sin (P + Q))$$

Comments (0)

Advertisement