We will consider three cases

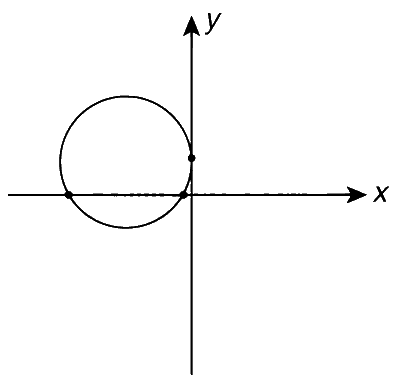
Case 1 : Circle passes through origin, that is, p = 0 the equation of circle becomes

x² + y² + 2x + 4y = 0

x = 0 $$\Rightarrow$$ y² + 4y = 0 $$\Rightarrow$$ y(y + 4) = 0

y = 0, $$-$$4

y = 0 $$\Rightarrow$$ x² + 2x = 0 $$\Rightarrow$$ x(x + 2) = 0 $$\Rightarrow$$ x = 0, $$-$$ 2

Case 2 : Circle touches y axis then circle will intersect x axis at two distinct points

Put y = 0 in equation of circle, we get

x² + 2x $$-$$ p = 0

Now from g² $$-$$ c > 0 and f² $$-$$ c = 0

$$\Rightarrow$$ 1² $$-$$ ($$-$$p) > 0 and 2² $$-$$ ($$-$$p) = 0

1 + p > 0 and 4 + p = 0

p > $$-$$1 and p = $$-$$ 4

which is a contradiction. Also, for p = $$-$$4 we get

x² $$-$$ 2x + 4 = 0

$$x = {{2 \pm \sqrt {4 - 4 \times 4} } \over 2} = {{2 \pm 2\sqrt 3 i} \over 2} = 1 \pm \sqrt 3 i$$

They are imaginary roots.

Therefore, Case 2 is not possible.

Case 3 : Circle touches x axis. Then the circle will intersect y axis at two distinct points.

Substituting x = 0, we get

y² + 4y $$-$$ p = 0

Now, from g² $$-$$ C = 0 and f² $$-$$ C > 0, we have

1² $$-$$ ($$-$$p) = 0 and 2² = ($$-$$p) > 0

p = $$-$$1 and 4 + p > 0 $$\Rightarrow$$ p > $$-$$4

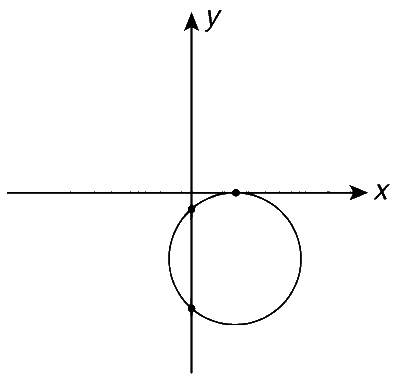
Therefore, the equation of circle becomes

y² + 4y + 1 = 0

$$ \Rightarrow y = {{ - 4 \pm \sqrt {16 - 4} } \over 2} = {{ - 4 \pm \sqrt {12} } \over 2}$$

$$y = {{ - 4 \pm \sqrt {4 \times 3} } \over 2}$$

$$ = {{ - 4 \pm 2\sqrt 3 } \over 2} = - 2 \pm \sqrt 3 $$ real values

Thus, Case 3 is possible.

Thus, for p = 0 and p = $$-$$1 the circle and coordinates have exactly three points in common. Hence, the correct answer is 2.