JEE Advance - Mathematics (2016 - Paper 2 Offline - No. 3)
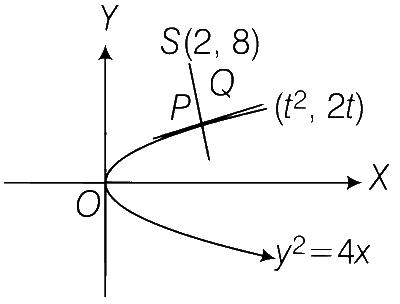
Let $$P$$ be the point on the parabola $${y^2} = 4x$$ which is at the shortest distance from the center $$S$$ of the circle $${x^2} + {y^2} - 4x - 16y + 64 = 0$$. Let $$Q$$ be the point on the circle dividing the line segment $$SP$$ internally. Then
$$SP = 2\sqrt 5 $$
$$SQ:QP = \left( {\sqrt 5 + 1} \right):2$$
the $$x$$-intercept of the normal to the parabola at $$P$$ is $$6$$
the slope of the tangent to the circle at $$Q$$ is $${1 \over 2}$$
Explanation
Tangent to y2 = 4x at (t2, 2t) is
y(2t) = 2(x + t2)
$$\Rightarrow$$ yt = x + t2 ...... (i)
Equation of normal at P(t2, 2t) is
y + tx = 2t + t3
Since, normal at P passes through centre of circle S(2, 8).
$$\therefore$$ 8 + 2t = 2t + t3 $$\Rightarrow$$ t = 2, i.e., P(4, 4)
$$\therefore$$ $$SP = \sqrt {{{(4 - 2)}^2} + {{(4 - 8)}^2}} = 2\sqrt 5 $$
$$\therefore$$ Option (a) is correct.
Also, SQ = 2
$$\therefore$$ PQ = SP $$-$$ SQ = 2$$\sqrt5$$ $$-$$ 2
Thus, $${{SQ} \over {QP}} = {1 \over {\sqrt 5 - 1}} = {{\sqrt 5 + 1} \over 4}$$
$$\therefore$$ Option (b) is incorrect.
Now, x-intercept of normal is
x = 2 + 22 = 6
$$\therefore$$ Option (c) is correct.
Slope of tangent $$ = {1 \over t} = {1 \over 2}$$
$$\therefore$$ Option (d) is correct.
Comments (0)


