$$f(x) = [{x^2} - 3] = [{x^2}] - 3$$

$$ = \left\{ {\matrix{ { - 3,} & { - 1/2 \le x < 1} \cr { - 2,} & {1 \le x < \sqrt 2 } \cr { - 1,} & {\sqrt 2 \le x < \sqrt 3 } \cr {0,} & {\sqrt 3 \le x < 2} \cr {1,} & {x = 2} \cr } } \right.$$

and $$g(x) = |x|f(x) + |4x - 7|f(x)$$

$$ = (|x| + |4x - 7|)f(x)$$

$$ = (|x| + |4x - 7|)[{x^2} - 3]$$

$$ = \left\{ {\matrix{ {( - x - 4x - 7)( - 3),} & { - 1/2 \le x < 0} \cr {(x - 4x + 7)( - 3),} & {0 \le x < 1} \cr {(x - 4x + 7)( - 2),} & {1 \le x < \sqrt 2 } \cr {(x - 4x + 7)( - 1),} & {\sqrt 2 \le x < \sqrt 3 } \cr {(x - 4x + 7)(0),} & {\sqrt 3 \le x < 7/4} \cr {(x + 4x - 7)(0),} & {7/4 \le x < 2} \cr {(x + 4x - 7)(1),} & {x = 2} \cr } } \right.$$

$$\therefore$$ $$g(x) = \left\{ {\matrix{ {15x + 21,} & { - 1/2 \le x < 0} \cr {9x - 21,} & {0 \le x < 1} \cr {6x - 14,} & {1 \le x < \sqrt 2 } \cr {3x - 7,} & {\sqrt 2 \le x\sqrt 3 } \cr {0,} & {\sqrt 3 \le x < 2} \cr {5x - 7,} & {x = 2} \cr } } \right.$$

Now, the graphs of f(x) and g(x) are shown below.

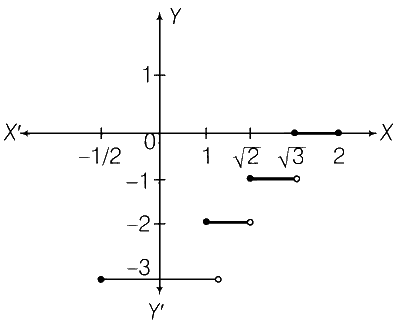
Graph for f(x)

Clearly, f(x) is discontinuous at 4 points.

$$\therefore$$ Option (b) is correct.

Graph for g(x)

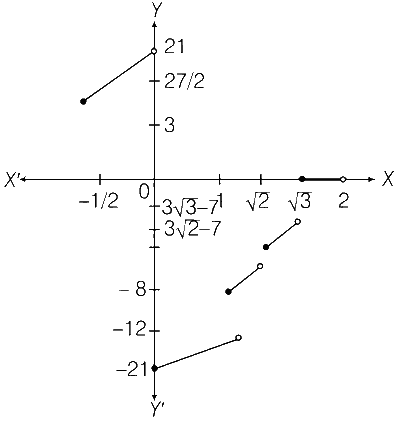
Clearly, g(x) is not differentiable at 4 points, when

x $$\in$$ ($$-$$1 / 2, 2).

$$\therefore$$ Option (c) is correct.