$$f(x) = \mathop {\lim }\limits_{n \to \infty } {\left\{ {{{{n^{2n}}\left( {{x \over n} + 1} \right)\left( {{x \over n} + {1 \over 2}} \right)...\left( {{x \over n} + {1 \over n}} \right)} \over {n!{n^{2n}}\left( {{{{x^2}} \over {{n^2}}} + 1} \right)\left( {{{{x^2}} \over {{n^2}}} + {1 \over {{2^2}}}} \right)....\left( {{{{x^2}} \over {{n^2}}} + {1 \over {{n^2}}}} \right)}}} \right\}^{{x \over n}}}$$

By taking logarithm we have

$$\ln f(x) = \mathop {\lim }\limits_{n \to \infty } {x \over n}\left\{ {\sum\limits_{r = 1}^n {\ln \left( {1 + {{rx} \over n}} \right) - \sum\limits_{r = 1}^n {\ln \left( {1 + {{{r^2}{x^2}} \over {{n^2}}}} \right)} } } \right\}$$

By definite integration, we can write it as

$$\ln f(x) = x\int\limits_0^1 {\ln (1 + xy)dy - x\int\limits_0^1 {\ln (1 + {x^2}{y^2})dy} } $$

Let xy = u

Then, $$\ln f(x) = \int\limits_0^x {\ln (1 + u)du - \int\limits_0^x {\ln (1 + {u^2})du} } $$

Using Newton-Leibnitz formula, we get

$${1 \over {f(x)}}\,.\,f'(x) = log\left( {{{1 + x} \over {1 + {x^2}}}} \right)$$ ...... (i)

Here, at x = 1,

$${{f'(1)} \over {f(1)}} = \log (1) = 0$$

$$\therefore$$ $$f'(1) = 0$$

Now, sign scheme of f'(x) is shown below

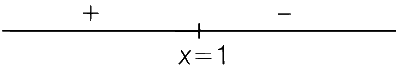
$$\therefore$$ At x = 1, function attains maximum. Since, f(x) increases on (0, 1).

$$\therefore$$ f(1) > f(1/2)

$$\therefore$$ Option (a) is incorrect.

f(1/3) < f(2/3)

$$\therefore$$ Option (b) is correct.

Also, f'(x) < 0, when x > 1

$$\Rightarrow$$ f'(2) < 0