Sign In

JEE Advance - Mathematics (2016 - Paper 1 Offline - No. 9)

The circle $${C_1}:{x^2} + {y^2} = 3,$$ with centre at $$O$$, intersects the parabola $${x^2} = 2y$$ at the point $$P$$ in the first quadrant, Let the tangent to the circle $${C_1}$$, at $$P$$ touches other two circles $${C_2}$$ and $${C_3}$$ at $${R_2}$$ and $${R_3}$$, respectively. Suppose $${C_2}$$ and $${C_3}$$ have equal radil $${2\sqrt 3 }$$ and centres $${Q_2}$$ and $${Q_3}$$, respectively. If $${Q_2}$$ and $${Q_3}$$ lie on the $$y$$-axis, then
$${Q_2}{Q_3} = 12$$
$${R_2}{R_3} = 4\sqrt 6 $$
area of the triangle $$O{R_2}{R_3}$$ is $$6\sqrt 2 $$
area of the triangle $$P{Q_2}{Q_3}$$ is $$4\sqrt 2 $$

Explanation

In case of option (A)

x2 + y2 = 3 and x2 = 2y

Solving we get $$P(\sqrt 2 ,1)$$

Equation of tangent at P on the circle

$$x\sqrt 2 + y = 3$$ $$\therefore$$ $$\tan \alpha = - \sqrt 2 $$

Again, $${{{Q_2}{R_2}} \over {{Q_2}M}} = \sin \left( {\alpha - {\pi \over 2}} \right)$$

or, $${{2\sqrt 3 } \over {{Q_2}M}} = - \cos \alpha = - {1 \over {\sqrt 3 }}$$ [$$\because$$ $$\tan \alpha = - \sqrt 2 $$]

or, $${Q_2}M = 6$$

Similarly, $${Q_3}M = 6$$

$$\therefore$$ $${Q_2}{Q_3} = 12$$

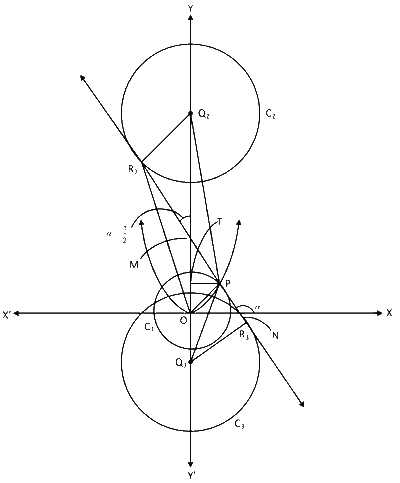
JEE Advanced 2016 Paper 1 Offline Mathematics - Parabola Question 39 English Explanation

In case of option (B)

$${{M{R_2}} \over {{Q_2}{R_2}}} = \tan \left( {\alpha - {\pi \over 2}} \right)$$

or, $${{M{R_2}} \over {2\sqrt 3 }} = - \tan \alpha = \sqrt 2 $$

or, $$M{R_2} = 2\sqrt 6 $$

Similarly, $$M{R_3} = 2\sqrt 6 $$ $$\therefore$$ $${R_2}{R_3} = 4\sqrt 6 $$

In case of option (C)

OP is the perpendicular drawn from O to R2R3

$$\therefore$$ area of $$\Delta O{R_2}{R_3} = {1 \over 2} \times OP \times {R_2}{R_3} = {1 \over 2} \times \sqrt 3 \times 4\sqrt 6 =6\sqrt 2 $$

In case of option (D)

PT is perpendicular drawn from P to Q2Q3

$$\therefore$$ area of $$\Delta P{Q_2}{Q_3} = {1 \over 2} \times PT \times {Q_2}{Q_3} = {1 \over 2} \times \sqrt 2 \times 12 = 6\sqrt 2 $$

Therefore, (A), (B), (C) are correct options.

Comments (0)

Advertisement