JEE Advance - Mathematics (2016 - Paper 1 Offline - No. 7)
In a triangle $$\Delta $$$$XYZ$$, let $$x, y, z$$ be the lengths of sides opposite to the angles $$X, Y, Z$$ respectively, and $$2s = x + y + z$$.
If $${{s - x} \over 4} = {{s - y} \over 3} = {{s - z} \over 2}$$ and area of incircle of the triangle $$XYZ$$ is $${{8\pi } \over 3}$$, then
If $${{s - x} \over 4} = {{s - y} \over 3} = {{s - z} \over 2}$$ and area of incircle of the triangle $$XYZ$$ is $${{8\pi } \over 3}$$, then
area of the triangle $$XYZ$$ is $$6\sqrt 6 $$
the radius of circumcircle of the triangle $$XYZ$$ is $${{35} \over 6}\sqrt 6 $$
$$\sin {X \over 2}\sin {Y \over 2}\sin {Z \over 2} = {4 \over {35}}$$
$${\sin ^2}\left( {{{X + Y} \over 2}} \right) = {3 \over 5}$$
Explanation
It is given that
$$ 2 s=x+y+z $$
Let us consider
$$ \frac{s-x}{4}=\frac{s-y}{3}=\frac{s-z}{2}=k $$
That is, $s=4 k+x$
$$ \begin{aligned} &s =3 k+y \\\\ &s =2 k+z \\\\ &3 s =9 k+(x+y+z)=9 k+2 s \\\\ &s =9 k \\\\ &x =9 k-4 k=5 k \\\\ &y =6 k, z=7 k \end{aligned} $$
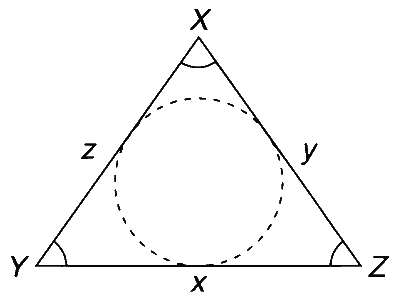
Area of in-circle of the triangle $X Y Z$ is
$$ \begin{aligned} \pi r^2 & =\pi\left(\frac{\Delta}{s}\right)^2 \\\\ & =\frac{\pi}{s^2} \Delta^2=\frac{\pi}{s^2} s(s-x)(s-y)(s-z) \\\\ & =\frac{\pi}{81 k^2} \times 9 k \times 4 k \times 3 k \times 2 k \\\\ & =\frac{\pi}{9 k} \times 24 k^3=\frac{\pi}{9} 24 k^2 \end{aligned} $$
$$ \begin{aligned} & \text {Therefore, } \frac{\pi}{9} 24 k^2=\frac{8 \pi}{3} \\\\ & \Rightarrow \quad k^2=\frac{8 \pi}{3} \times \frac{9}{24 \pi}=1 \Rightarrow k=1 \end{aligned} $$
The sides of the triangle is given by $x=5, y=6, z=7$. Now, the area of $\triangle X Y Z$ is
$$ \sqrt{s(s-x)(s-y)(s-z)}=\sqrt{9 \times 4 \times 3 \times 2}=6 \sqrt{6} $$
Hence, option $(\mathrm{A})$ is correct.
Now, $R=\frac{x y z}{4 \Delta}=\frac{5 \times 6 \times 7}{4 \times 6 \sqrt{6}}=\frac{35}{4 \sqrt{6}}$
$$ \begin{aligned} & \sin \frac{X}{2} \sin \frac{Y}{2} \sin \frac{Z}{2} \\\\ & \left.\quad=\sqrt{\left[\frac{(s-y)(s-z)}{y z}\right]\left[\frac{(s-z)(s-z)}{x z}\right]\left[\frac{(s-y)(s-x)}{x y}\right]}\right. \\\\ & \quad=\frac{(s-z)(s-y)(s-z)}{x y z} \\\\ & \text {Now, } \frac{(s-z)(s-y)(s-z)}{x y z}=\frac{4 \times 3 \times 2}{5 \times 6 \times 7}=\frac{4}{25} \end{aligned} $$
Hence, option (C) is correct.
Now, $\sin ^2\left(\frac{X+Y}{2}\right)=\sin ^2\left(\frac{\pi-Z}{2}\right)=\cos ^2 \frac{z}{2}=\frac{s(s-z)}{x y}$
$$ =\frac{9 \times 2}{5 \times 6}=\frac{3}{5} $$
Hence, option (D) is correct.
$$ 2 s=x+y+z $$
Let us consider
$$ \frac{s-x}{4}=\frac{s-y}{3}=\frac{s-z}{2}=k $$
That is, $s=4 k+x$
$$ \begin{aligned} &s =3 k+y \\\\ &s =2 k+z \\\\ &3 s =9 k+(x+y+z)=9 k+2 s \\\\ &s =9 k \\\\ &x =9 k-4 k=5 k \\\\ &y =6 k, z=7 k \end{aligned} $$

Area of in-circle of the triangle $X Y Z$ is
$$ \begin{aligned} \pi r^2 & =\pi\left(\frac{\Delta}{s}\right)^2 \\\\ & =\frac{\pi}{s^2} \Delta^2=\frac{\pi}{s^2} s(s-x)(s-y)(s-z) \\\\ & =\frac{\pi}{81 k^2} \times 9 k \times 4 k \times 3 k \times 2 k \\\\ & =\frac{\pi}{9 k} \times 24 k^3=\frac{\pi}{9} 24 k^2 \end{aligned} $$
$$ \begin{aligned} & \text {Therefore, } \frac{\pi}{9} 24 k^2=\frac{8 \pi}{3} \\\\ & \Rightarrow \quad k^2=\frac{8 \pi}{3} \times \frac{9}{24 \pi}=1 \Rightarrow k=1 \end{aligned} $$
The sides of the triangle is given by $x=5, y=6, z=7$. Now, the area of $\triangle X Y Z$ is
$$ \sqrt{s(s-x)(s-y)(s-z)}=\sqrt{9 \times 4 \times 3 \times 2}=6 \sqrt{6} $$
Hence, option $(\mathrm{A})$ is correct.
Now, $R=\frac{x y z}{4 \Delta}=\frac{5 \times 6 \times 7}{4 \times 6 \sqrt{6}}=\frac{35}{4 \sqrt{6}}$
$$ \begin{aligned} & \sin \frac{X}{2} \sin \frac{Y}{2} \sin \frac{Z}{2} \\\\ & \left.\quad=\sqrt{\left[\frac{(s-y)(s-z)}{y z}\right]\left[\frac{(s-z)(s-z)}{x z}\right]\left[\frac{(s-y)(s-x)}{x y}\right]}\right. \\\\ & \quad=\frac{(s-z)(s-y)(s-z)}{x y z} \\\\ & \text {Now, } \frac{(s-z)(s-y)(s-z)}{x y z}=\frac{4 \times 3 \times 2}{5 \times 6 \times 7}=\frac{4}{25} \end{aligned} $$
Hence, option (C) is correct.
Now, $\sin ^2\left(\frac{X+Y}{2}\right)=\sin ^2\left(\frac{\pi-Z}{2}\right)=\cos ^2 \frac{z}{2}=\frac{s(s-z)}{x y}$
$$ =\frac{9 \times 2}{5 \times 6}=\frac{3}{5} $$
Hence, option (D) is correct.
Comments (0)


