Options (A) and (B): The given differential equation is

$$ \left[x^2+4 x+4+y(x+2)\right] \frac{d y}{d x}-y^2=0 \quad(x>0) $$

which is further simplified as follows:

$$ \left[(x+2)^2+y(x+2)\right] \frac{d y}{d x}-y^2=0 $$

Substituting $x+2=t$, we get

$$ \frac{d x}{d y}=\frac{d t}{d y} $$

Now,

$$ (x+2)^2+y(x+2)-y^2 \frac{d x}{d y}=0 $$

That is,

$$ \begin{aligned} &t^2+y t-y^2 \frac{d t}{d y} =0 \\\\ &y^2 \frac{d t}{d y}-y t-t^2 =0 \\\\ &\frac{1}{t^2} \frac{d t}{d y}-\frac{1}{y t} =\frac{1}{y^2} \end{aligned} $$

Let $\frac{1}{t}=z$; therefore,

$$ \frac{d t}{d y}\left(-\frac{1}{t^2}\right)=\frac{d z}{d y} $$

Now,

$\begin{aligned} \frac{-d z}{d y}-\frac{z}{y} & =\frac{1}{y^2} \Rightarrow \frac{d z}{d y}+\frac{z}{y}=\frac{-1}{y^2} \\\\ \Rightarrow d(z y) & =\int-\frac{1}{y} d y \\\\ \Rightarrow z y & =-\ln |y|+\ln c \\\\ \Rightarrow \frac{y}{t} & =-\ln |y|+\ln c\end{aligned}$

$$ \Rightarrow \frac{y}{(x+2)}=-\ln |y|+\ln c ~~~~~...(1) $$

which passes through the point $(1,3)$. Therefore, from Eq. (1), we get

$$ \begin{aligned} &\frac{z}{3} =-\ln 3+c \Rightarrow c=\ln 3 e \\\\ &\frac{y}{x+2} =-\ln |y|+\ln 3 e=\ln \left(\frac{3 e}{|y|}\right) \\\\ &\frac{3 e}{|y|} =e^{y /(x+2)} \\\\ &3 e =|y| e^{y /(x+2)} \end{aligned} $$

Substituting $y=(x+2)$, we get $3 e=|x+2| e^1$

$$ |x+2|=3 \Rightarrow x+2=-3,3 \Rightarrow x=-5,1 $$

Therefore, $x=1$ (since $x \neq-5)$.


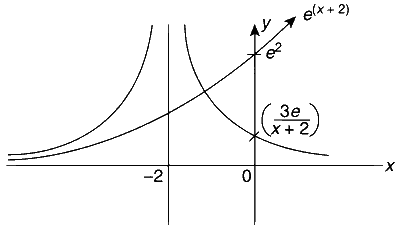
That is, the solution curve intersects $y=(x+2)$ exactly at one point and not at two points. Therefore, option (A) is correct and option (B) is incorrect.

Option (C): We have

$$ \frac{3 e}{\left|(x+2)^2\right|}=e^{(x+2)} $$

which meets at two points for $x<0$ and for $x>0$, there is no intersection point.

Hence, option $(\mathrm{C})$ is incorrect.

Option (D): We have

$$ \frac{3 e}{(x+3)^2}=e^{\frac{(x+3)^2}{(x+2)}}=e^{\frac{(x+2)^2+1+2(x+2)}{(x+2)}}=e^{2+\frac{1}{(x+2)}+(x+2)} $$

Therefore, there is no intersection point for $x>0$. Hence option (D) is correct.