JEE Advance - Mathematics (2016 - Paper 1 Offline - No. 2)
Consider a pyramid $$OPQRS$$ located in the first octant $$\left( {x \ge 0,y \ge 0,z \ge 0} \right)$$ with $$O$$ as origin, and $$OP$$ and $$OR$$ along the $$x$$-axis and the $$y$$-axis, respectively. The base $$OPQR$$ of the pyramid is a square with $$OP=3.$$ The point $$S$$ is directly above the mid-point, $$T$$ of diagonal $$OQ$$ such that $$TS=3.$$ Then
the acute angle between $$OQ$$ and $$OS$$ is $${\pi \over 3}$$
the equation of the plane containing the triangle $$OQS$$ is $$x-y=0$$
the length of the perpendicular from $$P$$ to the plane containing the triangle $$OQS$$ is $${3 \over {\sqrt 2 }}$$
the perpendicular distance from $$O$$ to the straight line containing $$RS$$ is $$\sqrt {{{15} \over 2}} $$
Explanation
Let us consider a pyramid OPQRS in the first octant with
O as origin as shown in the following figure:
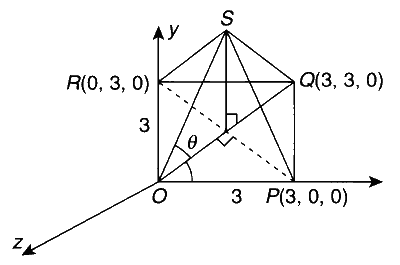
Now, the midpoint of $O Q$ is $T\left(\frac{3}{2}, \frac{3}{2}, 0\right)$.
Also, it is obvious that the point $S$ is given by $S\left(\frac{3}{2}, \frac{3}{2}, 3\right)$.
Now, $O T=\sqrt{\left(\frac{3}{2}\right)^2+\left(\frac{3}{2}\right)^2+0}=\frac{3}{2} \sqrt{2}$
Therefore, $\cos \theta=\frac{3}{2} \frac{\sqrt{2}}{3}=\frac{1}{\sqrt{2}} \Rightarrow \theta=\frac{\pi}{4}$
where $\theta$ is the angle between $O Q$ and $O S$, which is calculated as follows:
The ratio of the plane containing triangle $\triangle O Q S$ can be written as
$$ \left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 3 & 3 & 0 \\ 3 / 2 & 3 / 2 & 3 \end{array}\right|=i(9)-i(9)+k(0)=i(i-j) $$
Therefore, the ratio is $(1,-1,0)$.
Now, the equation of the plane is
$$ \begin{aligned} &1(x-0)-1(y-0)+0(z-0) =0 \\\\ &x-y =0 \end{aligned} $$
Hence, option (B) is correct.
The coordinates of the length of perpendicular from point $P$ to the plane $x-y=0$ is $(3,0,0)$.
Hence, the length of perpendicular from point $P$ to the plane containing the triangle $O Q S$ is
$$ \frac{z-0}{\sqrt{2}}=\frac{3}{\sqrt{2}} $$
Hence, option (C) is correct.
Now, points $R$ and $S$, respectively, are $R(0,3,0)$ and $$ S\left(\frac{3}{2}, \frac{3}{2}, 3\right) \text {. } $$
The equation of line $R S$ is
$$ \begin{aligned} \bar{r} & =3 \hat{j}+\lambda\left(\frac{3}{2} \hat{i}+\left(\frac{3}{2}-3\right) \hat{j}+3 \hat{k}\right) \\\\ & =3 \hat{j}+\lambda\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right) \end{aligned} $$
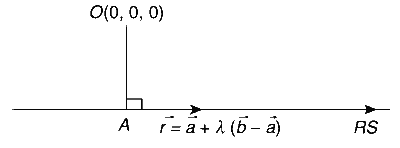
Let point A be the feet of perpendicular from O to line RS:
$$ \begin{aligned} & A\left(3 \hat{j}+\mu\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right)\right) \\\\ & \text {Now, } \overrightarrow{O A}=3 \hat{j}+\mu\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right) \end{aligned} $$
That is, $(\vec{b}-\vec{a})=\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right)$
Therefore,
$$ \overrightarrow{O A} \cdot(\vec{b}-\vec{a})=0 $$
$$ \begin{aligned} &\left(3 \hat{j}+\mu\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right)\right) \cdot\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right)=0 \\\\ &\frac{-9}{2}+\mu\left(\frac{9}{4}+\frac{9}{4}+9\right)=0 \\\\ &\frac{-9}{2}+\mu\left(\frac{9}{2}+9\right)=0 \\\\ &\Rightarrow-\frac{1}{2}+\mu\left(\frac{3}{2}\right)=0 \\\\ &\Rightarrow \mu=\frac{1}{3} \end{aligned} $$
Therefore, $A\left(3 \hat{j}+\frac{\hat{i}}{2}-\frac{\hat{j}}{2}+\hat{k}\right)=A\left(\frac{\hat{i}}{2}+\frac{5 \hat{j}}{2}+\hat{k}\right)$ and hence the perpendicular distance from point $O$ to the straight line containing the line $R S$ is
$$ |\overrightarrow{O A}|=\sqrt{\frac{1}{4}+\frac{25}{4}+\frac{4}{4}}=\sqrt{\frac{30}{4}}=\sqrt{\frac{15}{2}} $$
Hence, option (D) is correct.

Now, the midpoint of $O Q$ is $T\left(\frac{3}{2}, \frac{3}{2}, 0\right)$.
Also, it is obvious that the point $S$ is given by $S\left(\frac{3}{2}, \frac{3}{2}, 3\right)$.
Now, $O T=\sqrt{\left(\frac{3}{2}\right)^2+\left(\frac{3}{2}\right)^2+0}=\frac{3}{2} \sqrt{2}$
Therefore, $\cos \theta=\frac{3}{2} \frac{\sqrt{2}}{3}=\frac{1}{\sqrt{2}} \Rightarrow \theta=\frac{\pi}{4}$
where $\theta$ is the angle between $O Q$ and $O S$, which is calculated as follows:
The ratio of the plane containing triangle $\triangle O Q S$ can be written as
$$ \left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k} \\ 3 & 3 & 0 \\ 3 / 2 & 3 / 2 & 3 \end{array}\right|=i(9)-i(9)+k(0)=i(i-j) $$
Therefore, the ratio is $(1,-1,0)$.
Now, the equation of the plane is
$$ \begin{aligned} &1(x-0)-1(y-0)+0(z-0) =0 \\\\ &x-y =0 \end{aligned} $$
Hence, option (B) is correct.
The coordinates of the length of perpendicular from point $P$ to the plane $x-y=0$ is $(3,0,0)$.
Hence, the length of perpendicular from point $P$ to the plane containing the triangle $O Q S$ is
$$ \frac{z-0}{\sqrt{2}}=\frac{3}{\sqrt{2}} $$
Hence, option (C) is correct.
Now, points $R$ and $S$, respectively, are $R(0,3,0)$ and $$ S\left(\frac{3}{2}, \frac{3}{2}, 3\right) \text {. } $$
The equation of line $R S$ is
$$ \begin{aligned} \bar{r} & =3 \hat{j}+\lambda\left(\frac{3}{2} \hat{i}+\left(\frac{3}{2}-3\right) \hat{j}+3 \hat{k}\right) \\\\ & =3 \hat{j}+\lambda\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right) \end{aligned} $$
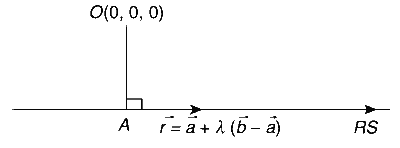
Let point A be the feet of perpendicular from O to line RS:
$$ \begin{aligned} & A\left(3 \hat{j}+\mu\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right)\right) \\\\ & \text {Now, } \overrightarrow{O A}=3 \hat{j}+\mu\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right) \end{aligned} $$
That is, $(\vec{b}-\vec{a})=\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right)$
Therefore,
$$ \overrightarrow{O A} \cdot(\vec{b}-\vec{a})=0 $$
$$ \begin{aligned} &\left(3 \hat{j}+\mu\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right)\right) \cdot\left(\frac{3}{2} \hat{i}-\frac{3}{2} \hat{j}+3 \hat{k}\right)=0 \\\\ &\frac{-9}{2}+\mu\left(\frac{9}{4}+\frac{9}{4}+9\right)=0 \\\\ &\frac{-9}{2}+\mu\left(\frac{9}{2}+9\right)=0 \\\\ &\Rightarrow-\frac{1}{2}+\mu\left(\frac{3}{2}\right)=0 \\\\ &\Rightarrow \mu=\frac{1}{3} \end{aligned} $$
Therefore, $A\left(3 \hat{j}+\frac{\hat{i}}{2}-\frac{\hat{j}}{2}+\hat{k}\right)=A\left(\frac{\hat{i}}{2}+\frac{5 \hat{j}}{2}+\hat{k}\right)$ and hence the perpendicular distance from point $O$ to the straight line containing the line $R S$ is
$$ |\overrightarrow{O A}|=\sqrt{\frac{1}{4}+\frac{25}{4}+\frac{4}{4}}=\sqrt{\frac{30}{4}}=\sqrt{\frac{15}{2}} $$
Hence, option (D) is correct.
Comments (0)


