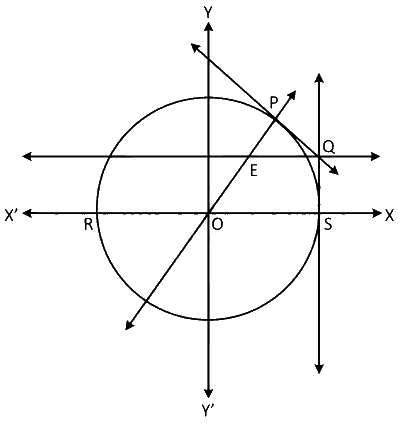
Let, P $$\equiv$$ (cos$$\theta$$, sin$$\theta$$)

$$\therefore$$ equation of tangent and normal at P

x cos$$\theta$$ + y sin$$\theta$$ = 1 ..... (1)

and y = x tan$$\theta$$ ...... (2)

Now, equation of tangent at S : x = 1 ...... (3)

Solving (1) and (3), Q $$\equiv$$ (1, cosec$$\theta$$ $$-$$ cot$$\theta$$)

$$\therefore$$ equation of straight line parallel to RS drawn from Q

y = cosec$$\theta$$ $$-$$ cot$$\theta$$ ..... (4)

Let, E $$\equiv$$ (h, k)

$$\therefore$$ k = h tan$$\theta$$ [from (2)]

or, $$\tan \theta = {k \over h}$$

Again, k = cosec$$\theta$$ $$-$$ cot$$\theta$$ [from (4)]

or, $$k = {{1 - \cos \theta } \over {\sin \theta }}$$

or, $$k = {{1 - {h \over {\sqrt {{h^2} + {k^2}} }}} \over {{k \over {\sqrt {{h^2} + {k^2}} }}}} = {{\sqrt {{h^2} + {k^2}} - h} \over k}$$

or, $${k^2} = \sqrt {{h^2} + {k^2}} - h$$

or, $$h + {k^2} = \sqrt {{h^2} + {k^2}} $$

$$\therefore$$ locus of E $$x + {y^2} = \sqrt {{x^2} + {y^2}} $$

Clearly, points $$\left( {{1 \over 3},{1 \over {\sqrt 3 }}} \right)$$ and $$\left( {{1 \over 3}, - {1 \over {\sqrt 3 }}} \right)$$ are on locus of E.

Therefore, (A) and (C) are the correct options.