JEE Advance - Mathematics (2015 - Paper 2 Offline - No. 5)
A ball is drawn at random from box $${\rm I}$$ and transferred to box $${\rm I}$$$${\rm I}.$$ If the probability of drawing a red ball from box $${\rm I},$$ after this transfer, is $${1 \over 3},$$ then the correct option(s) with the possible values of $${n_1}$$ and $${n_2}$$ is(are)
$${n_1} = 4$$ and $${n_2} = 6$$
$${n_1} = 2$$ and $${n_2} = 3$$
$${n_1} = 10$$ and $${n_2} = 20$$
$${n_1} = 3$$ and $${n_2} = 6$$
Explanation
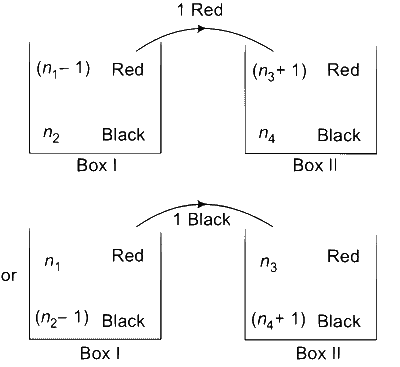
$$\therefore$$ P (drawing red ball from B1) = $${1 \over 3}$$
$$ \Rightarrow \left( {{{{n_1} - 1} \over {{n_1} + {n_2} - 1}}} \right)\left( {{{{n_1}} \over {{n_1} + {n_2}}}} \right) + \left( {{{{n_2}} \over {{n_1} + {n_2}}}} \right)\left( {{{{n_1}} \over {{n_1} + {n_2} - 1}}} \right) = {1 \over 3}$$
$$ \Rightarrow {{n_1^2 + {n_1}{n_2} - {n_1}} \over {({n_1} + {n_2})({n_1} + {n_2} - 1)}} = {1 \over 3}$$
Clearly, options (c) and (d) satisfy.
Comments (0)


