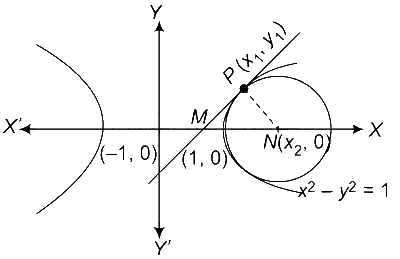
Equation of family of circles touching hyperbola at (x₁, y₁) is

(x $$-$$ x₁)² + (y $$-$$ y₁)² + $$\lambda$$(xx₁ $$-$$ yy₁ $$-$$ 1) =0

Now, its centre is (x₂, 0).

$$\therefore$$ $$\left[ {{{ - (\lambda {x_1} - 2{x_1})} \over 2},{{ - ( - 2{y_1} - \lambda {y_1})} \over 2}} \right] = ({x_2},0)$$

$$ \Rightarrow 2{y_1} + \lambda {y_1} = 0 \Rightarrow \lambda = - 2$$

and $$2{x_1} - \lambda x = 2{x_2} \Rightarrow {x_2} = 2{x_1}$$

$$\therefore$$ $$P({x_1},\sqrt {x_1^2 - 1} )$$

and $$N({x_2},0) = (2{x_1},0)$$

As tangent intersect X-axis at $$M\left( {{1 \over x},0} \right)$$.

Centroid of $$\Delta PWN = (l,m)$$

$$ \Rightarrow \left( {{{3{x_1} + {1 \over {{x_1}}}} \over 3},{{{y_1} + 0 + 0} \over 3}} \right) = (l,m)$$

$$ \Rightarrow l = {{3{x_1} + {1 \over {{x_1}}}} \over 3}$$

On differentiating w.r.t. x₁, we get

$${{dl} \over {d{x_1}}} = {{3 - {1 \over {x_1^2}}} \over 3}$$

$$ \Rightarrow {{dl} \over {d{x_1}}} = 1 - {1 \over {3x_2^1}}$$, for x₁ > 1

and $$m = {{\sqrt {x_1^2 - 1} } \over 3}$$

On differentiating w.r.t. x₁, we get

$${{dm} \over {d{x_1}}} = {{2{x_1}} \over {2 \times 3\sqrt {x_1^2 - 1} }} = {{{x_1}} \over {3\sqrt {x_1^2 - 1} }}$$, for x₁ > 1

Also, $$m = {{{y_1}} \over 3}$$

On differentiating w.r.t. y₁, we get

$${{dm} \over {d{y_1}}} = {1 \over 3}$$, for y₁ > 0