JEE Advance - Mathematics (2015 - Paper 1 Offline - No. 6)
Match the following :
| Column I | Column I | ||
|---|---|---|---|
| (A) | $\begin{array}{l}\text { In a triangle } \Delta X Y Z \text {, let } a, b \text { and } c \text { be the lengths of the sides } \\\text { opposite to the angles } X, Y \text { and } Z \text {, respectively. If } 2\left(a^2-b^2\right)=c^2 \\\text { and } \lambda=\frac{\sin (X-Y)}{\sin Z} \text {, then possible values of } n \text { for which } \cos (n \lambda) \\=0 \text { is (are) }\end{array}$ | (P) | 1 |
| (B) | $\begin{array}{l}\text { In a triangle } \triangle X Y Z \text {, let } a, b \text { and } c \text { be the lengths of the sides } \\\text { opposite to the angles } X, Y \text { and } Z \text {, respectively. If } 1+\cos 2 X-2 \\\cos 2 Y=2 \sin X \sin Y \text {, then possible value(s) of } \frac{a}{b} \text { is (are) }\end{array}$ | (Q) | 2 |
| (C) | $\begin{array}{l}\text { In } \mathbb{R}^2 \text {, let } \sqrt{3} \hat{i}+\hat{j}, \hat{i}+\sqrt{3} \hat{j} \text { and } \beta \hat{i}+(1-\beta) \hat{j} \text { be the position } \\\text { vectors of } X, Y \text { and } Z \text { with respect of the origin } \mathrm{O} \text {, respectively. If } \\\text { the distance of } \mathrm{Z} \text { from the bisector of the acute angle of } \overrightarrow{\mathrm{OX}} \text { with } \\\overrightarrow{\mathrm{OY}} \text { is } \frac{3}{\sqrt{2}} \text {, then possible value(s) of }|\beta| \text { is (are) }\end{array}$ | (R) | 3 |
| (D) | $\begin{array}{l}\text { Suppose that } F(\alpha) \text { denotes the area of the region bounded by } \\x=0, x=2, y^2=4 x \text { and } y=|\alpha x-1|+|\alpha x-2|+\alpha x \text {, } \\\text { where, } \alpha \in\{0,1\} \text {. Then the value(s) of } F(\alpha)+\frac{8}{2} \sqrt{2} \text {, when } \alpha=0 \\\text { and } \alpha=1 \text {, is (are) }\end{array}$ | (S) | 5 |
| (T) | 6 |
$$\left( A \right) \to P,R;\,\,\left( B \right) \to P;\,\,\left( C \right) \to P,Q;\,\,\left( D \right) \to S,T$$
$$\left( A \right) \to P,R,S;\,\,\left( B \right) \to P;\,\,\left( C \right) \to P,Q;\,\,\left( D \right) \to S,T$$
$$\left( A \right) \to P,R,S;\,\,\left( B \right) \to P;\,\,\left( C \right) \to P;\,\,\left( D \right) \to S,T$$
$$\left( A \right) \to S;\,\,\left( B \right) \to P;\,\,\left( C \right) \to P;\,\,\left( D \right) \to S,T$$
Explanation
Option (A):
$$ \begin{aligned} & 2\left(a^2-b^2\right)=c^2 \quad\quad(1)\\\\ & \lambda=\frac{\sin (x-y)}{\sin z} \quad\quad(2)\\\\ & \cos (n \pi \lambda)=0 \quad\quad(3)\\\\ & \Rightarrow n \lambda=\frac{(2 m+1)}{2}\quad\quad(4) \end{aligned} $$
From Eq. (2), we have
$$ \lambda=\frac{\sin x(0) y-\cos x \sin y}{\sin z} $$
$$ \begin{aligned} & \Rightarrow \lambda=\frac{a \cos y-b \cos x}{c} \\\\ & \Rightarrow \lambda=\frac{a\left(\frac{a^2+c^2-b^2}{2 a c}\right)-b\left(\frac{b^2+c^2-a^2}{2 b c}\right)}{2 c} \quad \text { (by sine formula) } \\\\ & \Rightarrow \lambda=\frac{2\left(a^2-b^2\right)}{2 c^2}=\frac{1}{2}\quad\quad(5) \end{aligned} $$
Therefore, from Eqs. (4) and (5), we get
$$ \frac{x}{2}=\frac{2 m+1}{2} \Rightarrow x=(2 m+1) $$
Hence, (A)→(P), (R), (S).
Option (B):
$$ \begin{aligned} & 1+\cos 2 x-2 \cos 2 y=2 \sin x \sin y \\\\ \Rightarrow & 2 \cos ^2 x-2\left(2 \cos ^2 y-1\right)=2 \sin x \sin y \\\\ \Rightarrow & 2 \cos ^2 x-4 \cos ^2 y+2=2 \sin x \sin y \\\\ \Rightarrow & 2 \sin ^2 y-2 \sin x \sin y+\sin x \sin y-\sin ^2 x=0 \\\\ \Rightarrow & 2 \sin y(\sin y-\sin x)+\sin x(\sin y-\sin x)=0 \\\\ \Rightarrow & (\sin y-\sin x)(2 \sin y+\sin x)=0 \\\\ \Rightarrow & b=a \text { or } 2 b=-a(\text { which is impossible }) \\\\ \Rightarrow & \frac{a}{b}=1 \end{aligned} $$
Hence, $(\mathrm{B}) \rightarrow(\mathrm{P})$
Option (C):
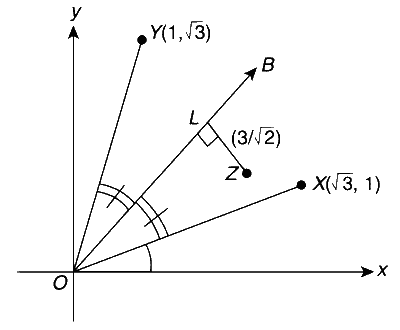
Vector along the bisector of acute angle between $\overrightarrow{O X}$ and $\overrightarrow{O Y}$ is
$$ \frac{\sqrt{3} \hat{i}+\hat{j}}{2}+\frac{\hat{i}+\sqrt{3} \hat{j}}{2}=\frac{(\sqrt{3}+1)}{2}(\hat{i}+\hat{j}) $$
Slope of $\overrightarrow{O B}=\tan \left(\frac{\pi}{4}\right)=1$
Equation of $O B$ is $y=x$.
Since
$$ \begin{aligned} Z L & =\frac{3}{\sqrt{3}} \Rightarrow \frac{|\beta-(1-\beta)|}{\sqrt{2}}=\frac{3}{\sqrt{2}} \\\\ & \Rightarrow|2 \beta-1|=3 \\\\ & \Rightarrow(2 \beta-1)= \pm 3 \\\\ & \Rightarrow \beta=2 \text { or } \beta=-1 \\\\ & \Rightarrow|\beta|=1 \text { or } 2 \end{aligned} $$
$(\mathrm{C}) \rightarrow(\mathrm{P}),(\mathrm{Q})$
Option (D):
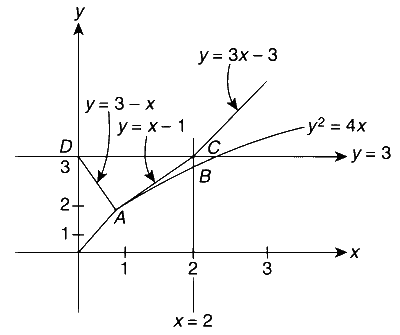
$$ \Rightarrow y=|\alpha x-1|+|\alpha x-2|+\alpha x ; \alpha \in\{0,1\} $$
Case (I): For $\alpha=0, y=3$
Case (II): For $\alpha=1, y=|x-1|+|x-2|+x$
$\Rightarrow y=\left\{\begin{array}{cc}3-x ; & x \leq 1 \\ x+1 ; & 1 < x < 2 \\ 3 x-3 ; & x \geq 2\end{array}\right.$
Hence,
$$ \begin{aligned} F(0) & =\int_0^2(3-2 \sqrt{x}) d x=\left[3 x-\frac{4}{3} x^{3 / 2}\right]_0^2 \\\\ & =\left[6-\frac{4}{3}(2 \sqrt{2})\right]=6-\frac{8}{3} \sqrt{2} \\\\ \Rightarrow & F(0)+\frac{8}{3} \sqrt{2}=6 \Rightarrow(T) \end{aligned} $$
and
$$ \begin{aligned} F(1) & =F(0)-\text { area of } \triangle A C D \\\\ & =\left(6-\frac{8}{3} \sqrt{2}\right)-\frac{1}{2}(2)(1)=5-\frac{8}{3} \sqrt{2} \\\\ & \Rightarrow F(1)+\frac{8}{3} \sqrt{2}=5 \Rightarrow(S) \end{aligned} $$
Hence, $(\mathrm{D}) \rightarrow(\mathrm{T}),(\mathrm{S})$
$$ \begin{aligned} & 2\left(a^2-b^2\right)=c^2 \quad\quad(1)\\\\ & \lambda=\frac{\sin (x-y)}{\sin z} \quad\quad(2)\\\\ & \cos (n \pi \lambda)=0 \quad\quad(3)\\\\ & \Rightarrow n \lambda=\frac{(2 m+1)}{2}\quad\quad(4) \end{aligned} $$
From Eq. (2), we have
$$ \lambda=\frac{\sin x(0) y-\cos x \sin y}{\sin z} $$
$$ \begin{aligned} & \Rightarrow \lambda=\frac{a \cos y-b \cos x}{c} \\\\ & \Rightarrow \lambda=\frac{a\left(\frac{a^2+c^2-b^2}{2 a c}\right)-b\left(\frac{b^2+c^2-a^2}{2 b c}\right)}{2 c} \quad \text { (by sine formula) } \\\\ & \Rightarrow \lambda=\frac{2\left(a^2-b^2\right)}{2 c^2}=\frac{1}{2}\quad\quad(5) \end{aligned} $$
Therefore, from Eqs. (4) and (5), we get
$$ \frac{x}{2}=\frac{2 m+1}{2} \Rightarrow x=(2 m+1) $$
Hence, (A)→(P), (R), (S).
Option (B):

$$ \begin{aligned} & 1+\cos 2 x-2 \cos 2 y=2 \sin x \sin y \\\\ \Rightarrow & 2 \cos ^2 x-2\left(2 \cos ^2 y-1\right)=2 \sin x \sin y \\\\ \Rightarrow & 2 \cos ^2 x-4 \cos ^2 y+2=2 \sin x \sin y \\\\ \Rightarrow & 2 \sin ^2 y-2 \sin x \sin y+\sin x \sin y-\sin ^2 x=0 \\\\ \Rightarrow & 2 \sin y(\sin y-\sin x)+\sin x(\sin y-\sin x)=0 \\\\ \Rightarrow & (\sin y-\sin x)(2 \sin y+\sin x)=0 \\\\ \Rightarrow & b=a \text { or } 2 b=-a(\text { which is impossible }) \\\\ \Rightarrow & \frac{a}{b}=1 \end{aligned} $$
Hence, $(\mathrm{B}) \rightarrow(\mathrm{P})$
Option (C):

Vector along the bisector of acute angle between $\overrightarrow{O X}$ and $\overrightarrow{O Y}$ is
$$ \frac{\sqrt{3} \hat{i}+\hat{j}}{2}+\frac{\hat{i}+\sqrt{3} \hat{j}}{2}=\frac{(\sqrt{3}+1)}{2}(\hat{i}+\hat{j}) $$
Slope of $\overrightarrow{O B}=\tan \left(\frac{\pi}{4}\right)=1$
Equation of $O B$ is $y=x$.
Since
$$ \begin{aligned} Z L & =\frac{3}{\sqrt{3}} \Rightarrow \frac{|\beta-(1-\beta)|}{\sqrt{2}}=\frac{3}{\sqrt{2}} \\\\ & \Rightarrow|2 \beta-1|=3 \\\\ & \Rightarrow(2 \beta-1)= \pm 3 \\\\ & \Rightarrow \beta=2 \text { or } \beta=-1 \\\\ & \Rightarrow|\beta|=1 \text { or } 2 \end{aligned} $$
$(\mathrm{C}) \rightarrow(\mathrm{P}),(\mathrm{Q})$
Option (D):

$$ \Rightarrow y=|\alpha x-1|+|\alpha x-2|+\alpha x ; \alpha \in\{0,1\} $$
Case (I): For $\alpha=0, y=3$
Case (II): For $\alpha=1, y=|x-1|+|x-2|+x$
$\Rightarrow y=\left\{\begin{array}{cc}3-x ; & x \leq 1 \\ x+1 ; & 1 < x < 2 \\ 3 x-3 ; & x \geq 2\end{array}\right.$
Hence,
$$ \begin{aligned} F(0) & =\int_0^2(3-2 \sqrt{x}) d x=\left[3 x-\frac{4}{3} x^{3 / 2}\right]_0^2 \\\\ & =\left[6-\frac{4}{3}(2 \sqrt{2})\right]=6-\frac{8}{3} \sqrt{2} \\\\ \Rightarrow & F(0)+\frac{8}{3} \sqrt{2}=6 \Rightarrow(T) \end{aligned} $$
and
$$ \begin{aligned} F(1) & =F(0)-\text { area of } \triangle A C D \\\\ & =\left(6-\frac{8}{3} \sqrt{2}\right)-\frac{1}{2}(2)(1)=5-\frac{8}{3} \sqrt{2} \\\\ & \Rightarrow F(1)+\frac{8}{3} \sqrt{2}=5 \Rightarrow(S) \end{aligned} $$
Hence, $(\mathrm{D}) \rightarrow(\mathrm{T}),(\mathrm{S})$
Comments (0)


