JEE Advance - Mathematics (2015 - Paper 1 Offline - No. 5)
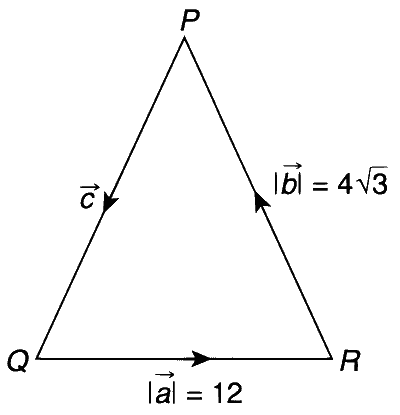
Let $$\Delta PQR$$ be a triangle. Let $$\vec a = \overrightarrow {QR} ,\vec b = \overrightarrow {RP} $$ and $$\overrightarrow c = \overrightarrow {PQ} .$$ If $$\left| {\overrightarrow a } \right| = 12,\,\,\left| {\overrightarrow b } \right| = 4\sqrt 3 ,\,\,\,\overrightarrow b .\overrightarrow c = 24,$$ then which of the following is (are) true?
$${{{{\left| {\overrightarrow c } \right|}^2}} \over 2} - \left| {\overrightarrow a } \right| = 12$$
$${{{{\left| {\overrightarrow c } \right|}^2}} \over 2} + \left| {\overrightarrow a } \right| = 30$$
$$\left| {\overrightarrow a \times \overrightarrow b + \overrightarrow c \times \overrightarrow a } \right| = 48\sqrt 3 $$
$$\overrightarrow a .\overrightarrow b = - 72$$
Explanation
For a triangle, we have $\vec{a}+\vec{b}+\vec{c}=\overrightarrow{0}$
$$ \begin{aligned} & \Rightarrow \vec{a}=-(\vec{b}+\vec{c}) \\\\ & \Rightarrow|\vec{a}|^2=|\vec{b}|^2+|\vec{c}|^2+2 \vec{b} \cdot \vec{c} \\\\ & \Rightarrow|\vec{a}|^2=48+|\vec{c}|^2+48 \\\\ & \Rightarrow|\vec{c}|^2=|\vec{a}|^2-96=144-96 \\\\ & \Rightarrow|\vec{c}|^2=48 \\\\ & \Rightarrow|\vec{c}|=\sqrt{48}=4 \sqrt{3} \end{aligned} $$
Therefore, $\frac{|\vec{c}|^2}{2}-|\vec{a}|=24-12=12$
Option (A) is correct.
$$ \frac{|\vec{c}|^2}{2}+|\vec{a}|=24+12=36 $$
Also, $\quad \vec{a}+\vec{b}=-\vec{c} \Rightarrow \vec{a} \cdot \vec{b}=-72$
From Eq. (1), we get
$$ \begin{aligned} & \vec{a} \times \vec{a}=-(\vec{a} \times \vec{b}+\vec{a} \times \vec{c}) \Rightarrow \vec{a} \times \vec{b}=\vec{c} \times \vec{a} \\\\ & |\vec{a} \times \vec{b}+\vec{a} \times \vec{c}|=|2(\vec{a} \times \vec{b})|=2|\vec{a}||\vec{b}| \sin \theta \\\\ & =96 \sqrt{3} \sqrt{1-\left(\frac{-72}{48 \sqrt{3}}\right)^2} \\\\ & =96 \sqrt{3} \sqrt{1-\left(\frac{\sqrt{3}}{12}\right)^2}=48 \sqrt{3} \end{aligned} $$

$$ \begin{aligned} & \Rightarrow \vec{a}=-(\vec{b}+\vec{c}) \\\\ & \Rightarrow|\vec{a}|^2=|\vec{b}|^2+|\vec{c}|^2+2 \vec{b} \cdot \vec{c} \\\\ & \Rightarrow|\vec{a}|^2=48+|\vec{c}|^2+48 \\\\ & \Rightarrow|\vec{c}|^2=|\vec{a}|^2-96=144-96 \\\\ & \Rightarrow|\vec{c}|^2=48 \\\\ & \Rightarrow|\vec{c}|=\sqrt{48}=4 \sqrt{3} \end{aligned} $$
Therefore, $\frac{|\vec{c}|^2}{2}-|\vec{a}|=24-12=12$
Option (A) is correct.
$$ \frac{|\vec{c}|^2}{2}+|\vec{a}|=24+12=36 $$
Also, $\quad \vec{a}+\vec{b}=-\vec{c} \Rightarrow \vec{a} \cdot \vec{b}=-72$
From Eq. (1), we get
$$ \begin{aligned} & \vec{a} \times \vec{a}=-(\vec{a} \times \vec{b}+\vec{a} \times \vec{c}) \Rightarrow \vec{a} \times \vec{b}=\vec{c} \times \vec{a} \\\\ & |\vec{a} \times \vec{b}+\vec{a} \times \vec{c}|=|2(\vec{a} \times \vec{b})|=2|\vec{a}||\vec{b}| \sin \theta \\\\ & =96 \sqrt{3} \sqrt{1-\left(\frac{-72}{48 \sqrt{3}}\right)^2} \\\\ & =96 \sqrt{3} \sqrt{1-\left(\frac{\sqrt{3}}{12}\right)^2}=48 \sqrt{3} \end{aligned} $$
Comments (0)


