JEE Advance - Mathematics (2014 - Paper 2 Offline - No. 3)
$$\,\,\,\,$$ $$\,\,\,\,$$ $$\,\,\,\,$$ List-$$I$$
(P.)$$\,\,\,\,$$ Let $$y\left( x \right) = \cos \left( {3{{\cos }^{ - 1}}x} \right),x \in \left[ { - 1,1} \right],x \ne \pm {{\sqrt 3 } \over 2}.$$ Then $${1 \over {y\left( x \right)}}\left\{ {\left( {{x^2} - 1} \right){{{d^2}y\left( x \right)} \over {d{x^2}}} + x{{dy\left( x \right)} \over {dx}}} \right\}$$ equals
(Q.)$$\,\,\,\,$$ Let $${A_1},{A_2},....,{A_n}\left( {n > 2} \right)$$ be the vertices of a regular polygon of $$n$$ sides with its centre at the origin. Let $${\overrightarrow {{a_k}} }$$ be the position vector of the point $${A_k},k = 1,2,......,n.$$
$$$f\left| {\sum\nolimits_{k = 1}^{n - 1} {\left( {\overrightarrow {{a_k}} \times \overrightarrow {{a_{k + 1}}} } \right)} } \right| = \left| {\sum\limits_{k = 1}^{n - 1} {\left( {\overrightarrow {{a_k}} .\,\overrightarrow {{a_{k + 1}}} } \right)} } \right|,$$$
then the minimum value of $$n$$ is
(R.)$$\,\,\,\,$$ If the normal from the point $$P(h, 1)$$ on the ellipse $${{{x^2}} \over 6} + {{{y^2}} \over 3} = 1$$ is perpendicular to the line $$x+y=8,$$ then the value of $$h$$ is
(S.)$$\,\,\,\,$$ Number of positive solutions satisfying the equation $${\tan ^{ - 1}}\left( {{1 \over {2x + 1}}} \right) + {\tan ^{ - 1}}\left( {{1 \over {4x + 1}}} \right) = {\tan ^{ - 1}}\left( {{2 \over {{x^2}}}} \right)$$ is
$$\,\,\,\,$$ $$\,\,\,\,$$ $$\,\,\,\,$$List-$$II$$
(1.)$$\,\,\,\,$$ $$1$$
(2.)$$\,\,\,\,$$ $$2$$
(3.)$$\,\,\,\,$$ $$8$$
(4.)$$\,\,\,\,$$ $$9$$
Explanation
$$\begin{aligned} & \text { (P) Given } y(x)=\cos \left(3 \cos ^{-1} x\right), x \in[-1,1] \\ & \Rightarrow \quad y(x)=4 \cos ^3\left(\cos ^{-1} x\right)-3 \cos \left(\cos ^{-1} x\right) \\ & \Rightarrow \quad y(x)=4 x^3-3 x \quad \text{... (i)}\\ & \Rightarrow \quad \frac{d y(x)}{d x}=12 x^2-3 \quad \text{... (ii)}\\ & \Rightarrow \quad \frac{d^2 y(x)}{d x^2}=24 x \quad \text{... (iii)}\\ \end{aligned}$$
From equation (i), (ii) and (iii)
$$\begin{aligned} \Rightarrow & \frac{1}{y(x)}\left[\left(x^2-1\right) \frac{d^2 y(x)}{d x^2}+x \frac{d y(x)}{d x}\right] \\ & =\frac{1}{4 x^3-3 x}\left[\left(x^2-1\right) \cdot 24 x+x \cdot\left(12 x^2-3\right)\right] \\ & =\frac{1}{4 x^3-3 x}\left[24 x^3-24 x+12 x^3-3 x\right] \\ & =\frac{1}{4 x^3-3 x}\left[36 x^3-27 x\right] \end{aligned}$$
$$\begin{aligned} & =\frac{9\left(4 x^3-3 x\right)}{4 x^3-3 x} \\ & =9 \end{aligned}$$
Hence P match with 4
(Q) Given $$\mathrm{A}_1, \mathrm{~A}_2, \mathrm{~A}_3, \ldots . \mathrm{A}_n(n>2)$$ be the vertices of a regular polygon of $$n$$ sides with centre at origin and $$\vec{a}_k$$ be the position vector of the point $$A_k$$
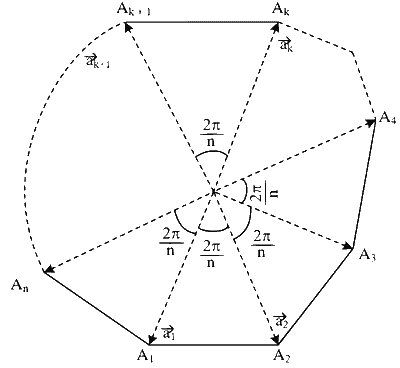
$$\begin{aligned} & \text { Here, } \begin{aligned} &\left|\vec{a}_1\right|=\left|\vec{a}_2\right|=\left|\vec{a}_3\right|=\ldots=\left|\vec{a}_k\right| \\ &=\left|\vec{a}_{k+1}\right|=\cdots=\left|\vec{a}_n\right|=\lambda \text { (let) } \\ & \text { And } \angle \mathrm{A}_1 \mathrm{OA}_2=\angle \mathrm{A}_2 \mathrm{OA}_3=\cdots=\angle \mathrm{A}_k \mathrm{OA}_{k+1} \\ &=\cdots=\angle \mathrm{A}_n \mathrm{OA}_1=\frac{2 \pi}{n} \\ & \Rightarrow \vec{a}_k \times \vec{a}_{k+1}=\lambda \cdot \lambda \cdot \sin \frac{2 \pi}{n} \cdot \hat{p} \text { and } \\ & \vec{a}_k \cdot \vec{a}_{k+1}=\lambda \cdot \lambda \cdot \cos \frac{2 \pi}{n} \end{aligned} \end{aligned}$$
Apply $$\left|\sum_\limits{k=1}^{n-1} \vec{a}_k \times \vec{a}_{k+1}\right|=\left|\sum_\limits{k=1}^{n-1} \vec{a}_k \cdot \vec{a}_{k+1}\right|$$
$$\begin{aligned} & \left|\sum_{k=1}^{n-1} \lambda^2 \sin \frac{2 \pi}{n} \hat{p}\right|=\left|\sum_{k=1}^{n-1} \lambda^2 \cos \frac{2 \pi}{n}\right| \\ & \Rightarrow(n-1) \lambda^2\left|\sin \frac{2 \pi}{n}\right|=(n-1) \lambda^2\left|\cos \frac{2 \pi}{n}\right| \\ & \Rightarrow\left|\tan \frac{2 \pi}{n}\right|=1 \\ & \Rightarrow n_{\text {min }}=8 \\ \end{aligned}$$
Hence $$Q$$ match with 3 .
(R) We know the equation of normal of ellipse $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$ at $$\left(x_1, y_1\right)$$ is $$\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2$$.
$$\therefore$$ Equation of Normal of ellipse $$\frac{x^2}{6}+\frac{y^2}{3}=1$$ at $$p(h, 1)$$ is $$\frac{6 x}{h}-\frac{3 y}{1}=1$$
Given, the normal at $$p(h, 1)$$ is perpendicular to the line $$x+y=3$$
$$\Rightarrow \quad \frac{{\frac{6}{h}}}{3} \times(-1)=-1$$
$$\Rightarrow \quad \frac{2}{h}=1$$
$$\Rightarrow \quad h=2$$
Hence, R match with 2.
$$\begin{aligned} & \text { (S) } \tan ^{-1}\left(\frac{1}{2 x+1}\right)+\tan ^{-1}\left(\frac{1}{4 x+1}\right)=\tan ^{-1} \frac{2}{x^2} \\ & \Rightarrow \quad \tan ^{-1}\left(\frac{\frac{1}{2 x+1}+\frac{1}{4 x+1}}{1-\frac{1}{2 x+1} \times \frac{1}{4 x+1}}\right)=\tan ^{-1}\left(\frac{2}{x^2}\right) \\ & \Rightarrow \quad \tan ^{-1}\left(\frac{6 x+2}{8 x^2+6 x+1-1}\right)=\tan ^{-1}\left(\frac{2}{x^2}\right) \\ & \Rightarrow \quad \tan ^{-1}\left(\frac{3 x+1}{4 x^2+3 x}\right)=\tan ^{-1}\left(\frac{2}{x^2}\right) \end{aligned}$$
$$\begin{aligned} & \Rightarrow & 3 x^3+x^2 & =8 x^2+6 x \\ & \Rightarrow & x\left[3 x^2-7 x-6\right] & =0 \\ & \Rightarrow & x\left[3 x^2-9 x+2 x-6\right] & =0 \\ & \Rightarrow & x(3 x+2)(x-3) & =0 \\ & \Rightarrow & x & =0, \frac{-2}{3}, 3 \end{aligned}$$
So, $$x=3$$ is the only positive solution of given equation.
Hence, S match with 1.
Hint:
(i) Recall $$\cos \left(\cos ^{-1} x\right)=x \forall x \in[-1,1]$$ and $$\cos 3 \theta=4 \cos ^3 \theta-3 \cos \theta$$
(ii) If angle between $$\vec{a}$$ and $$\vec{b}$$ is $$\theta$$, then $$\vec{a} \cdot \vec{b}=|\vec{a}||\vec{b}| \cos \theta$$ and $$\vec{a} \times \vec{b}=|\vec{a}||\vec{b}| \sin \theta \hat{n}$$
(iii) The equation of normal of ellipse $$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$$ at $$\left(x_1, y_1\right)$$ is $$\frac{a^2 x}{x_1}-\frac{b^2 y}{y_1}=a^2-b^2$$.
(iv) Recall $$\tan ^{-1} \mathrm{~A}+\tan ^{-1} \mathrm{~B}=\tan ^{-1}\left(\frac{\mathrm{A}+\mathrm{B}}{1-\mathrm{AB}}\right)$$ only when A.B < 1
Comments (0)


