$$\text { Given } f_2(x)=x^2 \text { for } x \in[0, \infty) \text { and co-domain } \mathrm{R} \text {. }$$

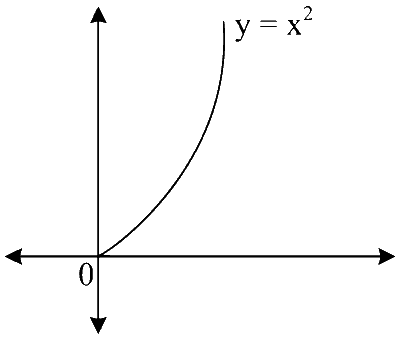
It is clear that $$f_2(x)$$ is continuous, differential and one-one but not onto because range of $$f_2(x)$$ is $$[0, \infty)$$ and given co-domain is R.

Hence $$S$$ match with 4.

Given, $$f_3(x)=\left\{\begin{array}{cc}\sin x, & \text { if } x<0 \\ x, & \text { if } x \geq 0\end{array}\right.$$. Domain of $$f_2(x)$$ is $$R$$ and co-domain $$R$$.

Draw the graph of $$f_3(x)$$

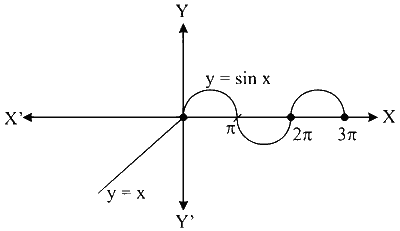
Range of $$f_3(x) \in(-\infty, 1] \neq$$ co-domain of $$f_3(x)$$

So, $$f_3(x)$$ is not onto.

$$\because \sin x$$ is not one-one function for $$x \geq 0$$

$$\therefore f_3(x)$$ is not one-one function.

We know $$y=\sin x$$ and $$y=x$$ both are continuous in the given domain.

At $$\quad x=0$$

$$\begin{aligned} \lim _{x \rightarrow 0^{+}} f_3(x) & =\lim _{x \rightarrow 0^{+}} \sin x=0 \\ \lim _{x \rightarrow 0^{-}} f_3(x) & =\lim _{x \rightarrow 0^{-}} x=0 \\ f_3(0) & =\sin 0=0 \\ \Rightarrow \lim _{x \rightarrow 0^{+}} f_3(x) & =\lim _{x \rightarrow 0^{-}} f_3(x)=f_3(0) \end{aligned}$$

$$\therefore f_3(x)$$ is continuous for all $$x \in \mathrm{R}$$.

We know that $$y=\sin x$$ and $$y=x$$ both are differentiable in the given domain R.H.D at $$x=0$$ is

$$\lim _\limits{h \rightarrow 0} \frac{f_3(0+h)-f_3(0)}{h}=\lim _\limits{h \rightarrow 0} \frac{\sin h-0}{h}=1$$

L.H.D at $$x=0$$ is

$$\lim _\limits{h \rightarrow 0} \frac{f_3(0-h)-f_3(0)}{-h}=\lim _\limits{h \rightarrow 0} \frac{-h-0}{-h}=1$$

$$\Rightarrow$$ R.H.D $$=$$ L.H.D at $$x=0$$

$$\therefore f_3(x)$$ is differentiable for all $$x \in R$$.

Hence, Q match with 3.

Now, $$f_2{ }^{\circ} f_1(x)= \begin{cases}x^2, & x<0 \\ e^{2 x}, & x \geq 0\end{cases}$$

Draw the graph of $$y=f_2{ }^{\circ} f_1(x)$$

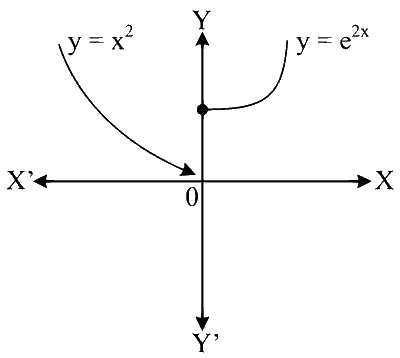
It is clear that $$f_2{ }^{\circ} f_1(x)$$ is neither continuous nor one-one.

Hence, R match with 2.

Given, $$f_4: \mathrm{R} \rightarrow[0, \infty)$$ and

$$f_4(x)=\left\{\begin{array}{l} f_2\left(f_1(x)\right), \text { if } x<0 \\ f_2\left(f_1(x)\right)-1, \text { if } x \geq 0 \end{array}\right.$$

Draw the graph of $$y=f_4(x)$$

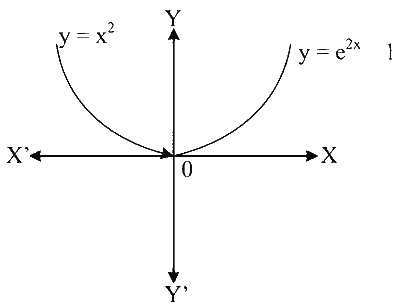
Range of $$f_4(x)=$$ co-domain of $$f_4(x)=[0, \infty)$$

$$\therefore \quad f_4(x)$$ is an onto function

$$f_4(x)$$ is continuous, on to but not one-one.

Hence, P match with 1.

Hint:

(i) If $$f(x)$$ is continuous at $$x=a$$, if and only if $$\lim _\limits{x \rightarrow a^{+}} f(x)=\lim _\limits{x \rightarrow a^{-}} f(x)=f(a)$$.

(ii) If $$f(x)$$ is differentiable at $$x=a$$ if and only if $$\lim _\limits{h \rightarrow 0} \frac{f(a+h)-f(a)}{h}=\lim _\limits{h \rightarrow 0} \frac{f(a-h)-f(a)}{-h}$$.

(iii) If Range of $$f(x)=\operatorname{co-domain}$$ of $$f(x)$$, then $$f(x)$$ is called an onto function.

(iv) If $$f\left(x_1\right)=f\left(x_2\right)$$ is possible only for $$x_1=x_2$$, then $$f(x)$$ is called an one-one function.