$$\begin{aligned} & \text { Given, } \sin x+2 \sin 2 x-\sin 3 x=3 \quad \text{... (i)}\\ & \Rightarrow \quad-[\sin 3 x-\sin x]+2 \sin 2 x=3 \end{aligned}$$

We know

$$\begin{aligned} & \sin \mathrm{C}-\sin \mathrm{D}=2 \cos \left(\frac{\mathrm{C}+\mathrm{D}}{2}\right) \cdot \sin \left(\frac{\mathrm{C}-\mathrm{D}}{2}\right) \\ & \text { and } \sin 2 \theta=2 \sin \theta \cdot \cos \theta \\ & \therefore-2 \cos \left(\frac{3 x+x}{2}\right) \cdot \sin \left(\frac{3 x-x}{2}\right)+2 \cdot 2 \sin x \cdot \cos x=3 \\ & \Rightarrow \quad-2 \cos 2 x \cdot \sin x+4 \sin x \cdot \cos x=3 \\ & \Rightarrow \quad-2 \sin x[\cos 2 x-2 \cos x]=3 \\ & \Rightarrow \quad-2 \sin x\left[2 \cos ^2 x-1-2 \cos x\right]=3 \\ & \Rightarrow \quad-4 \sin x\left[\cos ^2 x-2 \cdot \frac{1}{2} \cos x+\left(\frac{1}{2}\right)^2-\left(\frac{1}{2}\right)^2-\frac{1}{2}\right]=3 \end{aligned}$$

$$\begin{array}{lr} \Rightarrow & -4 \sin x\left[\left(\cos x-\frac{1}{2}\right)^2-\frac{3}{4}\right]=3 \\ \Rightarrow & -4 \sin x\left(\cos x-\frac{1}{2}\right)^2+3 \sin x=3 \\ \Rightarrow & 3 \sin x-3=4 \sin x\left(\cos x-\frac{1}{2}\right)^2 \end{array}$$

Draw the graph of $$y=3 \sin x-3$$ and $$y=\left(\cos x-\frac{1}{2}\right)^2$$ in the interval $$x \in(0, \pi)$$

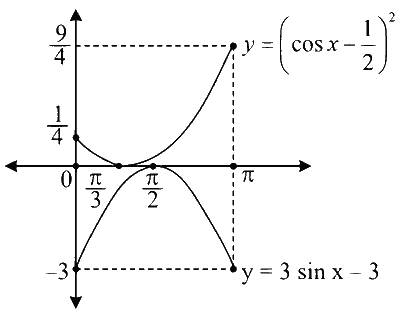
It is clear that the graphs $$y=3 \sin x-3$$ and $$y=\left(\cos x-\frac{1}{2}\right)$$ does not intersect in $$x \in(0, \pi)$$ Hence, the given equation $$\sin x+2 \sin 2 x-\sin 3 x=3$$ does not have any solution in the interval $$x \in(0, \pi)$$

Hint:

(i) Recall the formula $$\sin 2 x=2 \sin x \cdot \cos x, \cos 2 x=2 \cos ^2 x-1$$ and $$\sin \mathrm{C}-\sin \mathrm{D}=2 \cos \left(\frac{\mathrm{C}+\mathrm{D}}{2}\right) \cdot \sin \left(\frac{\mathrm{C}-\mathrm{D}}{2}\right)$$

(ii) The number of point of intersection of graphs of $$y=f(x)$$ and $$y=g(x)$$ is equal to the number of solution of $$f(x)=g(x)$$ in the given interval.