Given, four points $$\mathrm{P}\left(a t^2, 2 a t\right), \mathrm{Q}, \mathrm{R}\left(a r^2, 2 a r\right)$$ and $$S\left(a s^2, 2 a s\right)$$ be distinct points on the parabola $$y^2=4 a x$$.

Also given PQ is the focal chord of parabola

$$\begin{aligned} & y^2=4 a x \\ & \therefore \quad \mathrm{Q}=\left(\frac{a}{t^2},-\frac{2 a}{t}\right) \end{aligned}$$

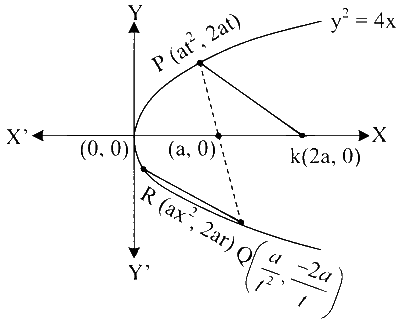
Given, $$\mathrm{K}=(2 a, 0)$$ and PK is parallel to QR

$$\therefore$$ Slope of line PK $$=$$ Slope of line QR

$$\begin{aligned} & \frac{2 a t-0}{a t^2-2 a}=\frac{2 a r+\frac{2 a}{t}}{a r^2-\frac{a}{t^2}} \\ \Rightarrow & \frac{t}{t^2-2}=\frac{r+\frac{1}{t}}{r^2-\frac{1}{t^2}} \\ \Rightarrow & \frac{t}{t^2-2}=\frac{r+\frac{1}{t}}{\left(r+\frac{1}{t}\right)\left(r-\frac{1}{t}\right)} \\ \Rightarrow & \frac{t}{t^2-2}=\frac{1}{r-\frac{1}{t}} \\ \Rightarrow & t r-1=t^2-2 \\ \Rightarrow & \quad r=\frac{t^2-1}{t} \end{aligned}$$

Hint:

(i) If PQ is a focal chord of parabola $$y^2=4 a x$$ and $$\mathrm{P}=\left(a t^2, 2 a t\right)$$, then $$\mathrm{Q}=\left(\frac{a}{t^2},-\frac{2 a}{t}\right)$$.

(ii) If two lines are parallel, then their slopes are equal.

(iii) The slope of line passing through two points $$\left(x_1, y_1\right)$$ and $$\left(x_2, y_2\right)$$ is $$\frac{y_2-y_1}{x_2-x_1}$$.