Given, a circle $$x^2+y^2=2$$ and a parabola $$y^2=8 x$$

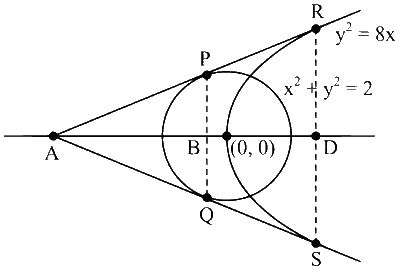
Let $$P R$$ and $$Q R$$ are common tangents of given circle and parabola intersect at A.

Let $$\mathrm{R}=\left(2 t^2, 4 t\right)$$ and $$S=\left(2 t^2,-4 t\right)$$

Equation of tangent of parabola

$$y^2=8 x \text { at } \mathrm{R}\left(2 t^2, 4 t\right) \text { is } t y=x+2 t^2$$

Here, $$A$$ is the point of intersection of tangent

$$\begin{aligned} t y & =x+2 t^2 \text { and } X \text {-axis } \\ \Rightarrow \mathrm{A} & =\left(-2 t^2, 0\right) \end{aligned}$$

Here, $$t y=x+2 t^2$$ also touches the circle at P

$$\begin{array}{lr} \therefore & \sqrt{2}=\frac{\left|0-t \times 0+2 t^2\right|}{\sqrt{1^2+(-t)^2}} \\ \Rightarrow & \sqrt{2} \cdot \sqrt{1+t^2}=2 t^2 \\ \Rightarrow & 2+2 t^2=4 t^4 \\ \Rightarrow & 2 t^4-t^2-1=0 \\ \Rightarrow & 2 t^4-2 t^2+t^2-1=0 \\ \Rightarrow & \left(2 t^2+1\right)\left(t^2-1\right)=0 \\ \Rightarrow & t^2=\frac{-1}{2}, 1 \end{array}$$

$$\begin{array}{ll} \Rightarrow t^2=1 \left(t^2=-\frac{1}{2} \text { is impossible }\right) \\ \Rightarrow t = \pm 1 \end{array}$$

$$\therefore \quad \mathrm{R}=(2,4), \mathrm{S}=(2,-4) \text { and } \mathrm{A}=(-2,0)$$

Now, the equation of chord PQ w.r.t. point $$(-2,0)$$ is

$$\begin{aligned} \Rightarrow & & -2 \cdot x+0 \cdot y-2 & =0 \\ \Rightarrow & & x & =-1 \end{aligned}$$

Here, P and Q are the point of intersection of circle $$x^2+y^2=2$$ and the line $$x=-1$$

$$\begin{aligned} & \therefore & (-1)^2+y^2 & =2 \\ \Rightarrow & & y & = \pm 1 \\ \Rightarrow & & P & =(-1,1) \text { and } \mathrm{Q}=(-1,-1) \end{aligned}$$

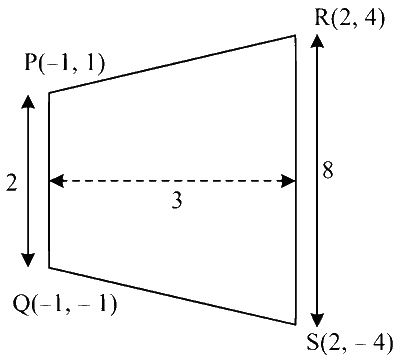
Area of quadrilateral $$\mathrm{PQRS}=\frac{1}{2} \times 3 \times(2+8) =15$$ Sq. units.

Hint:

(i) The parametric point of the parabola $$y^2=4 a x$$ is $$\left(a t^2, 2 a t\right)$$

(ii) Equation of tangent of the parabola $$y^2=4 a x$$ at $$\left(a t^2, 2 a t\right)$$ is $$t y=x+a t^2$$

(iii) If a line $$a x+b y+c=0$$ touches the circle $$\left(x-x_1\right)^2+\left(y-y_1\right)^2=R^2$$, then

$$\mathrm{R}=\frac{\left|a x_1+b y_1+\mathrm{C}\right|}{\sqrt{a^2+b^2}}$$