JEE Advance - Mathematics (2014 - Paper 1 Offline - No. 20)
Let f : R $$\to$$ R and g : R $$\to$$ R be respectively given by f(x) = | x | + 1 and g(x) = x2 + 1. Define h : R $$\to$$ R by $$h(x) = \left\{ {\matrix{
{\max \{ f(x),g(x)\} ,} & {if\,x \le 0.} \cr
{\min \{ f(x),g(x)\} ,} & {if\,x > 0.} \cr
} } \right.$$
The number of points at which h(x) is not differentiable is
The number of points at which h(x) is not differentiable is
Answer
3
Explanation
Concept :
The points at which the curve taken a sharp turn, are the points of non-differentiability.
Curve of f(x) and g(x) are
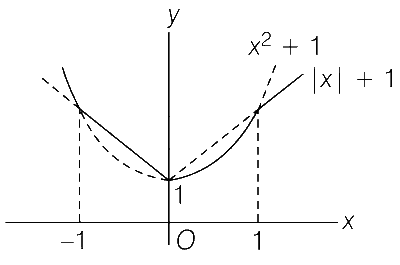
h(x) is not differentiable at x = $$\pm$$1 and 0.
As h(x) take sharp turns at x = $$\pm$$ 1 and 0.
Hence, number of points of non-differentiability of h(x) is 3.
The points at which the curve taken a sharp turn, are the points of non-differentiability.
Curve of f(x) and g(x) are

h(x) is not differentiable at x = $$\pm$$1 and 0.
As h(x) take sharp turns at x = $$\pm$$ 1 and 0.
Hence, number of points of non-differentiability of h(x) is 3.
Comments (0)


