Sign In

JEE Advance - Mathematics (2013 - Paper 2 Offline - No. 7)

Let $$f:\left[ {0,1} \right] \to R$$ (the set of all real numbers) be a function. Suppose the function $$f$$ is twice differentiable,
$$f(0) = f(1)=0$$ and satisfies $$f''\left( x \right) - 2f'\left( x \right) + f\left( x \right) \ge .{e^x},x \in \left[ {0,1} \right]$$.

If the function $${e^{ - x}}f\left( x \right)$$ assumes its minimum in the interval $$\left[ {0,1} \right]$$ at $$x = {1 \over 4}$$, which of the following is true?

$$f'\left( x \right) < f\left( x \right),{1 \over 4} < x < {3 \over 4}$$
$$f'\left( x \right) > f\left( x \right),0 < x < {1 \over 4}$$
$$f'\left( x \right) < f\left( x \right),0 < x < {1 \over 4}$$
$$f'\left( x \right) < f\left( x \right),{3 \over 4} < x < 1$$

Explanation

Given, $$e^{-x} f(x)$$ has point of minima at $$x=\frac{1}{4}$$ in the interval $$x \in[0,1]$$

Also given $$f(0)=f(1)=0$$

$$\begin{aligned} & \text { And } f^{\prime \prime}(x)-2 f^{\prime}(x)+f(x) \geq e^x, x \in[0,1] \\ & \Rightarrow e^{-x} f^{\prime \prime}(x)-e^{-x} f^{\prime}(x)-e^{-x} f^{\prime}(x)+e^{-x} f(x) \geq 1 \\ & \Rightarrow\left(e^{-x} f^{\prime}(x)\right)^{\prime}-\left(e^{-x} f(x)\right)^{\prime} \geq 1 \\ & \Rightarrow\left(e^{-x} f^{\prime}(x)-e^{-x} f(x)\right)^{\prime} \geq 1 \\ & \Rightarrow\left(e^{-x} f(x)\right)^{\prime \prime} \geq 1>0 \end{aligned}$$

Hence, the concavity of $$e^{-x} f(x)$$ is upward and given $$x=\frac{1}{4}$$ is the point of local minima of $$e^{-x} f(x)$$ in $$x \in[0,1]$$

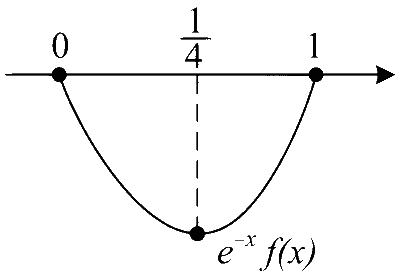
JEE Advanced 2013 Paper 2 Offline Mathematics - Application of Derivatives Question 21 English Explanation

$$\therefore e^{-x} f(x)$$ is decreasing in $$x \in\left(0, \frac{1}{4}\right)$$ and increasing in $$x \in\left(\frac{1}{4}, 1\right)$$

$$\Rightarrow\left(e^{-x} f(x)\right)^{\prime}<0$$ in $$x \in\left(0, \frac{1}{4}\right)$$ and $$\left(e^{-x} f(x)\right)^{\prime}>0$$ in $$x \in\left(\frac{1}{4}, 1\right)$$

$$\Rightarrow e^{-x} f^{\prime}(x)-e^{-x} f(x)<0$$ in $$x \in$$

$$\therefore e^{-x} f(x)$$ is decreasing in $$x \in\left(0, \frac{1}{4}\right)$$ and increasing in $$x \in\left(\frac{1}{4}, 1\right)$$

$$\Rightarrow\left(e^{-x} f(x)\right)^{\prime}<0, x \in\left(0, \frac{1}{4}\right)$$ and

$$\left(e^{-x} f(x)\right)^{\prime}>0, x \in\left(\frac{1}{4}, 1\right)$$

$$\Rightarrow e^{-x} f^{\prime}(x)-e^{-x} f(x)<0, x \in\left(0, \frac{1}{4}\right)$$ and

$$e^{-x} f^{\prime}(x)-e^{-x} f(x)>0, \quad x \in\left(\frac{1}{4}, 1\right)$$

$$\Rightarrow f^{\prime}(x) < f(x), x \in\left(0, \frac{1}{4}\right)$$ and

$$f^{\prime}(x) > f(x), x \in\left(\frac{1}{4}, 1\right)$$

Hints :

$$\Rightarrow e^{-x} f(x)$$ is minimum at $$x=\frac{1}{4}$$ in $$x \in\left[0, \frac{1}{4}\right]$$ implies $$e^{-x} f(x)$$ is decreasing in $$x \in\left[0, \frac{1}{4}\right]$$ and $$e^{-x} f(x)$$ is increasing in $$x \in\left(\frac{1}{4}, 1\right)$$.

Comments (0)

Advertisement