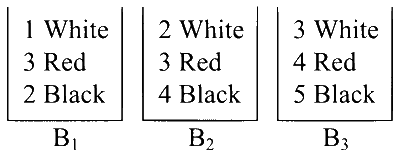
$$\begin{aligned} & \text { Let } \mathrm{P} \text { be the probability of same colour balls } \\ & \text { drawn from each boxes } \mathrm{B}_1, \mathrm{~B}_2, \mathrm{~B}_3 \\ & \therefore \quad \mathrm{P}=\mathrm{P} \text { (all are white) }+\mathrm{P} \text { (all are red) }+\mathrm{P} \text { (all } \\ & \quad \text { are Black) } \\ & \Rightarrow P=\frac{1}{6} \times \frac{2}{9} \times \frac{3}{12}+\frac{3}{6} \times \frac{3}{9} \times \frac{4}{12}+\frac{2}{6} \times \frac{4}{9} \times \frac{5}{12} \\ & \Rightarrow P=\frac{6}{648}+\frac{36}{648}+\frac{40}{648} \\ & \Rightarrow P=\frac{82}{648} \end{aligned}$$

Hints:

The probability of one ball is drawn from each boxes $$B_1, B_2, B_3$$ is equal to the sum of probabilities of all are white balls, all are red balls and all are Black balls.