Given two line

$$\mathrm{L}_1: \frac{x-5}{0}=\frac{y}{3-\alpha}=\frac{z}{-2}$$ and

$$\mathrm{L}_2: \frac{x-\alpha}{0}=\frac{y}{-1}=\frac{z}{2-\alpha}$$

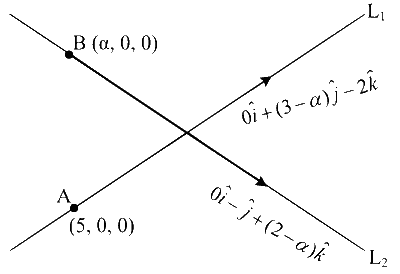
$$\Rightarrow \overrightarrow{\mathrm{AB}}=(\alpha-5) \hat{i}+0 \hat{j}+0 \hat{k}$$

$$\therefore \quad \mathrm{L}_1$$ and $$\mathrm{L}_2$$ are coplanar

$$\therefore$$ The scalar triple product of $$\overrightarrow{\mathrm{AB}}, 0 \hat{i}+(3-\alpha) \hat{j}-2 \hat{k}$$ and $$0 \hat{i}-\hat{j}+(2-\alpha) \hat{k}$$ is zero.

$$\begin{aligned} & \\ \Rightarrow \quad & \left|\begin{array}{ccc} \alpha-5 & 0 & 0 \\ 0 & 3-\alpha & -2 \\ \alpha & -1 & (2-\alpha) \end{array}\right|=0 \\ \Rightarrow \quad & (\alpha-5)[(3-\alpha)(2-\alpha)-2]=0 \\ \Rightarrow \quad & (\alpha-5)\left(\alpha^2-5 \alpha+4\right)=0 \\ \Rightarrow \quad & (\alpha-5)(\alpha-1)(\alpha-4)=0 \\ \Rightarrow \quad & \alpha=1,4,5 \end{aligned}$$

Hints :

If two line $$\frac{x-x_1}{a_1}=\frac{y-y_1}{b_1}=\frac{z-z_1}{c_1}$$ and $$\frac{x-x_2}{a_2}=\frac{y-y_2}{b_2}=\frac{z-z_2}{c_2}$$ are coplanar, then $$\left|\begin{array}{ccc}x_1-x_2 & y_1-y_2 & y_2-y_3 \\ a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2\end{array}\right|=0$$