JEE Advance - Mathematics (2013 - Paper 2 Offline - No. 20)
The function $$f(x) = 2\left| x \right| + \left| {x + 2} \right| - \left| {\left| {x + 2} \right| - 2\left| x \right|} \right|$$ has a local minimum or a local maximum at x =
$$-$$2
$${{ - 2} \over 3}$$
2
$${{ 2} \over 3}$$
Explanation
Here, $$f(x) = 2\left| x \right| + \left| {x + 2} \right| - \left| {\left| {x + 2} \right| - 2\left| x \right|} \right|$$
$$ = \left\{ {\matrix{ { - 2x - (x + 2) + (x - 2),} & {when\,x \le - 2} \cr { - 2x + x + 2 + 3x + 2,} & {when\, - 2 < x \le - {2 \over 3}} \cr { - 4x,} & {when\, - {2 \over 3} < x \le 0} \cr {4x,} & {when\,0 < x \le 2} \cr {2x + 4,} & {when\,x > 2} \cr } } \right.$$
$$ = \left\{ {\matrix{ { - 2x - 4,} & {x \le - 2} \cr {2x + 4,} & { - 2 < x \le - 2/3} \cr { - 4x,} & { - {2 \over 3} < x \le 0} \cr {4x,} & {0 < x \le 2} \cr {2x + 4,} & {x > 2} \cr } } \right.$$
Graph for y = f(x) is shown as
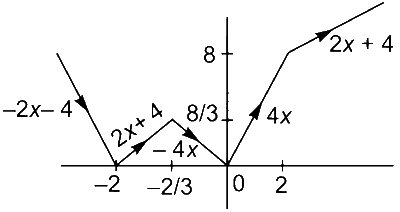
Comments (0)


